题目内容
3.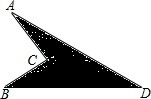 如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积.
如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积.
分析 先利用勾股定理求出AB,然后利用勾股定理的逆定理判断出△ABD是直角三角形,然后分别求出两个三角形的面积,相减即可求出阴影部分的面积.
解答 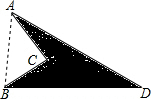 解:连接AB,
解:连接AB,
∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵AD=13,BD=12,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,
阴影部分的面积=$\frac{1}{2}$AB×BD-$\frac{1}{2}$AC×BC=30-6=24.
答:阴影部分的面积是24.
点评 此题考查了勾股定理勾股定理的逆定理,属于基础题,解答本题的关键是判断出三角形ABD为直角三角形.

练习册系列答案
相关题目
8.若一次函数y=(m-7)x-2的图象经过第二、三、四象限,则m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m>7 | D. | m<7 |
13.有四根细木棒,长度分别为3cm,5cm,7cm,9cm,则随机抽出三根木棒,能够组成三角形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
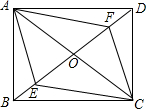 如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.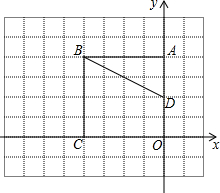 如图,在直角坐标系中,A(0,4),B(-4,4),C(-4,0),D(0,2).
如图,在直角坐标系中,A(0,4),B(-4,4),C(-4,0),D(0,2).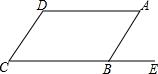 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C,∠D的度数.
如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C,∠D的度数.