题目内容
14.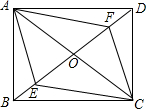 如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.(1)求证:四边形AECF是平行四边形;
(2)若OA=OD,则四边形ABCD是什么特殊四边形?请证明你的结论.
分析 (1)根据平行线的性质推出∠AFO=∠CEO,∠FAO=∠ECO,求出OE=OF,证△AOF≌△COE,推出AF=CE,根据平行四边形的判定推出即可;
(2)根据全等得出OA=OC,求出AC=BD,再根据平行四边形和矩形的判定推出即可.
解答 (1)证明:∵AF∥CE,
∴∠AFO=∠CEO,∠FAO=∠ECO,
∵O为BD的中点,即OB=OD,BE=DF,
∴OB-BE=OD-DF,即OE=OF,
在△AOF和△COE中
$\left\{\begin{array}{l}{∠AFO=∠CEO}\\{∠FAO=∠ECO}\\{OE=OF}\end{array}\right.$
∴△AOF≌△COE(AAS),
∴AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)若OA=OD,则四边形ABCD是矩形,
证明:∵△AOF≌△COE,
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形.
∵OA=OD,∴OA=OB=OC=OD,即BD=AC,
∴四边形ABCD为矩形.
点评 本题考查了平行四边形的性质和判定,矩形的判定,全等三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键,注意:对角线相等的平行四边形是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.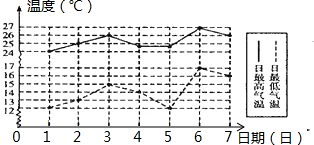 如图是某城市6月份1日至7日每天的最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
如图是某城市6月份1日至7日每天的最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
 如图是某城市6月份1日至7日每天的最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
如图是某城市6月份1日至7日每天的最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )| A. | 6月1日 | B. | 6月2日 | C. | 6月3日 | D. | 6月5日 |
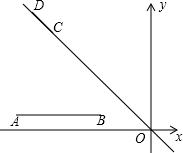 已知线段AB,且A(-8,1)、B(-3,1),另有一线段CD在直线y=-x上,且CD=$\sqrt{2}$,确定D点位置,使A、B、C、D构成的四边形周长最短,并求D点坐标及这个最小值.
已知线段AB,且A(-8,1)、B(-3,1),另有一线段CD在直线y=-x上,且CD=$\sqrt{2}$,确定D点位置,使A、B、C、D构成的四边形周长最短,并求D点坐标及这个最小值. 已知:△ABC在直角坐标系中,A(-4,4),B(-4,0),C(-2,0)
已知:△ABC在直角坐标系中,A(-4,4),B(-4,0),C(-2,0)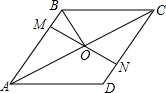 如图,在?ABCD中,对角线AC平分∠BAD,MN与AC交于点O,M,N分别在AB,CD上,且AM=CN,连接BO.若∠DAC=28°,则∠OBC的度数为62°.
如图,在?ABCD中,对角线AC平分∠BAD,MN与AC交于点O,M,N分别在AB,CD上,且AM=CN,连接BO.若∠DAC=28°,则∠OBC的度数为62°.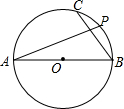 如图,在⊙O中,AB是直径,BC是弦,点P是$\widehat{BC}$上任意一点.若AB=10,BC=6,则AP的长不可能是( )
如图,在⊙O中,AB是直径,BC是弦,点P是$\widehat{BC}$上任意一点.若AB=10,BC=6,则AP的长不可能是( ) 如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.
如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2-14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒. 如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积.
如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积. 甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )
甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )