题目内容
13.有四根细木棒,长度分别为3cm,5cm,7cm,9cm,则随机抽出三根木棒,能够组成三角形的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
分析 利用列举法得到所有四种可能的结果数,再根据三角形三边的关系得到能够组成三角形的结果数,然后根据概率公式求解.
解答 解:从四根细木棒中随机抽出三根木棒,所有结果为3、5、7,3、5、9,3、7、9,5、7、9,其中能够组成三角形的结果数为3,
所有能够组成三角形的概率=$\frac{3}{4}$.
故选D.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了三角形三边的关系.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
1.在△ABC中,已知∠A=2∠B=3∠C,则三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 形状无法确定 |
5.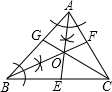 如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
 如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )| A. | AE、BF是△ABC的内角平分线 | B. | 点O到△ABC三边的距离相等 | ||
| C. | CG也是△ABC的一条内角平分线 | D. | AO=BO=CO |
 如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积.
如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积. 甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )
甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( ) 如图:在平面直角坐标系中,点A的坐标(2,4),点B的坐标(0,4),将△AOB绕点O旋转90°至△COD位置(其中点C与点A是对应点,点D与点B是对应点),OD落在x轴上,则点C的坐标是(4,-2),(-4,2).
如图:在平面直角坐标系中,点A的坐标(2,4),点B的坐标(0,4),将△AOB绕点O旋转90°至△COD位置(其中点C与点A是对应点,点D与点B是对应点),OD落在x轴上,则点C的坐标是(4,-2),(-4,2).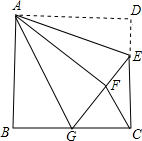 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形;⑤S△CFG=$\frac{18}{5}$.其中正确的结论是①②③⑤.(只填序号).
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形;⑤S△CFG=$\frac{18}{5}$.其中正确的结论是①②③⑤.(只填序号). 如图,在平面直角坐标系中,直线y=x与直线y=-2x+3交于点P,直线y=-2x+3与x轴交于点A,与y轴交于B.
如图,在平面直角坐标系中,直线y=x与直线y=-2x+3交于点P,直线y=-2x+3与x轴交于点A,与y轴交于B.