题目内容
14.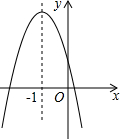 已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )
已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )①a<0,b<0,c<0;②b2-4ac>0;③2a-b=0;④ac>0;⑤a+b<0.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 ①根据抛物线与y轴交于y轴正半轴可知c>0,由此得出①不成立;②由函数图象与x轴交于两点,可知△=b2-4ac>0,由此得出②成立;③由抛物线对称轴为x=-$\frac{b}{2a}$=-1,可得出b=2a,由此得出③成立;④由①可知a<0,c>0,由此可得出④不成立;⑤由③b=2a可知a+b=3a<0,由此得出⑤成立.综上即可得出结论.
解答 解:①∵抛物线开口向下,且抛物线与y轴交点在y轴正半轴,
∴a<0,c>0,
∴a<0,c>0,①不成立;
②∵函数图象与x轴有两个交点,
∴△=b2-4ac>0,②成立;
③∵抛物线的对称轴为x=-$\frac{b}{2a}$=-1,
∴b=2a,
∴2a-b=0,③成立;
④由①的a<0,c>0,
∴ac<0,④不成立;
⑤由③知b=2a,
∴a+b=3a<0,⑤成立.
综上可知:②③⑤成立.
故选B.
点评 本题考查了二次函数图象与系数的关系,解题的关键是结合图象逐条分析结论.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的图象,结合开口、对称轴以及根的判别式去判定系数之间的关系.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
4.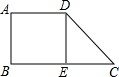 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )| A. | 24 | B. | 8$\sqrt{3}$ | C. | 36 | D. | 48 |
2.(-2)-3的值等于( )
| A. | 6 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |