题目内容
4.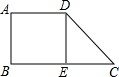 如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )
如图,在四边形ABCD中,∠C=45°,DE⊥BC于点E,若CE=4$\sqrt{3}$,四边形ABED为正方形,则四边形ABED的面积为( )| A. | 24 | B. | 8$\sqrt{3}$ | C. | 36 | D. | 48 |
分析 由已知条件易证△DEC是等腰直角三角形,所以DE=CE,进而可求出四边形ABED的面积.
解答 解:∵四边形ABED为正方形,
∴∠DEB=90°,
∴∠DEC=90°,
∵∠C=45°,
∴∠EDC=45°,
∴DE=CE=4$\sqrt{3}$,
∴四边形ABED的面积=4$\sqrt{3}$×4$\sqrt{3}$=48.
故选D.
点评 本题考查了正方形的性质、等腰直角三角形的判定和性质以及正方形面积公式的运用,求出正方形的边长是解题的关键.

练习册系列答案
相关题目
14. 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
19.下列式子中,不属于二次根式的是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{{a}^{2}}$ | C. | $\sqrt{-7}$ | D. | $\sqrt{\frac{1}{2}}$ |
9. 如图①所示,有一个由传感器A控制的灯,要装在门上方离地高4.5m的墙上,任何东西只要移至该灯5m及5m以内时,灯就会自动发光.请问一个身高1.5m的学生要走到离墙多远的地方灯刚好发光?( )
如图①所示,有一个由传感器A控制的灯,要装在门上方离地高4.5m的墙上,任何东西只要移至该灯5m及5m以内时,灯就会自动发光.请问一个身高1.5m的学生要走到离墙多远的地方灯刚好发光?( )
 如图①所示,有一个由传感器A控制的灯,要装在门上方离地高4.5m的墙上,任何东西只要移至该灯5m及5m以内时,灯就会自动发光.请问一个身高1.5m的学生要走到离墙多远的地方灯刚好发光?( )
如图①所示,有一个由传感器A控制的灯,要装在门上方离地高4.5m的墙上,任何东西只要移至该灯5m及5m以内时,灯就会自动发光.请问一个身高1.5m的学生要走到离墙多远的地方灯刚好发光?( )| A. | 4米 | B. | 3米 | C. | 5米 | D. | 7米 |
16. 如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
 如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )| A. | △AOB | B. | △COB | C. | △COD | D. | △AOD |
13.九年级数学兴趣小组经过市场调查,得到某种运动服进价为每件60元,每月的销量与售价的相关信息如表:
设该运动服的售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价x(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量y(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
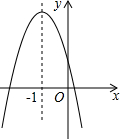 已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )
已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )