题目内容
9.纸片△ABC中,∠B=60°,AB=8cm,AC=7cm,将它折叠,使A与B重合,则折痕长为$\frac{12\sqrt{3}}{13}$或$\frac{20\sqrt{3}}{11}$cm.分析 当△ABC是锐角三角形时,如图1中,EF是折痕,作CM⊥AB垂足为M,作AH⊥BC于H,再求出BH、CH,在RT△BCM中QC BM、CM,再根据EF∥CM得$\frac{EF}{CM}$=$\frac{AE}{AM}$,由此即可解决.
当△ABC是钝角三角形时,如图2中,EF是折痕,作CM⊥AB垂足为M,作AH⊥BC于H,方法同上.
解答 解:当△ABC是锐角三角形时,如图1中,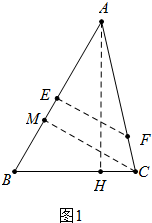 EF是折痕,作CM⊥AB垂足为M,作AH⊥BC于H,
EF是折痕,作CM⊥AB垂足为M,作AH⊥BC于H,
在RT△ABH中,∵∠AHB=90°,∠B=60°,AB=8,
∴BH=$\frac{1}{2}$AB=4,AH=$\sqrt{3}$BH=4$\sqrt{3}$,
在RT△AHC中,∠AHC=90°,AH=4$\sqrt{3}$,AC=7,
∴HC=$\sqrt{A{C}^{2}-A{H}^{2}}$=$\sqrt{{7}^{2}-(4\sqrt{3})^{2}}$=1,
∴BC=5,
在RT△BCM中,∵∠CMB=90°,∠B=60°,BC=5,
∴BM=$\frac{1}{2}BC$=$\frac{5}{2}$,MC=$\frac{5}{2}$$\sqrt{3}$,
∵EF∥CM,AE=EB=4,
∴$\frac{EF}{CM}$=$\frac{AE}{AM}$,
∴$\frac{EF}{\frac{5}{2}\sqrt{3}}$=$\frac{4}{\frac{11}{2}}$,
∴EF=$\frac{20\sqrt{3}}{11}$.
当△ABC是钝角三角形时,如图2中,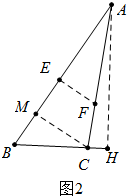 EF是折痕,作CM⊥AB垂足为M,作AH⊥BC于H,
EF是折痕,作CM⊥AB垂足为M,作AH⊥BC于H,
由(1)可知,BH=4,AH=4$\sqrt{3}$,CH=1,
∴BC=BH-CH=3,
在RT△BCM中,∵∠CMB=90°,∠B=60°,BC=3,
∴BM=$\frac{1}{2}BC$=$\frac{3}{2}$,MC=$\frac{3\sqrt{3}}{2}$,
∵EF∥CM,AE=EB=4,
∴$\frac{EF}{CM}$=$\frac{AE}{AM}$,
∴$\frac{EF}{\frac{3\sqrt{3}}{2}}$=$\frac{4}{\frac{13}{2}}$,
∴EF=$\frac{12\sqrt{3}}{13}$.
故答案为$\frac{12\sqrt{3}}{13}$或$\frac{20\sqrt{3}}{11}$
点评 本题考查翻折变换、30度直角三角形的性质、勾股定理、平行线分线段成比例定理等知识,解题的关键是添加辅助线构造直角三角形,学会应用平行线分线段成比例定理求线段的长,属于中考常考题型.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| A. | $\sqrt{5}$ | B. | $\sqrt{{a}^{2}}$ | C. | $\sqrt{-7}$ | D. | $\sqrt{\frac{1}{2}}$ |
| A. | 圆周角等于圆心角的一半 | B. | 等弧所对的圆周角相等 | ||
| C. | 平分弦的直径垂直于弦 | D. | 过弦的中点的直线必经过圆心 |
| A. | 5=ab | B. | 2+5=7 | C. | $\frac{x}{2}$+1=x+3 | D. | 3x+5y=8 |
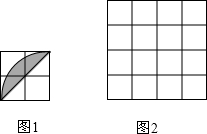 已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形.
已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形.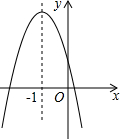 已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )
已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )