题目内容
6.已知圆锥的母线长5,底面半径为3,则圆锥的侧面积为15π,圆锥侧面展开图形的圆心角是216度.分析 圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解,根据弧长公式求出圆心角.
解答 解:圆锥的侧面积=2π×3×5÷2=15π,
圆锥的底面周长=2π×3=6π;
扇形圆心角=$\frac{180×6π}{π×5}$=216°.
故答案为:15π;216.
点评 本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
 如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,?ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )| A. | △AOB | B. | △COB | C. | △COD | D. | △AOD |
1.下列方程中是一元一次方程的是( )
| A. | 5=ab | B. | 2+5=7 | C. | $\frac{x}{2}$+1=x+3 | D. | 3x+5y=8 |
11.下列各式中一定是二次根式的是( )
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{x}$ | C. | $\root{3}{27}$ | D. | $\sqrt{{x}^{2}-2}$ |
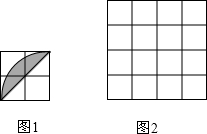 已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形.
已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形.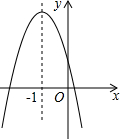 已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )
已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )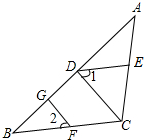 如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,