题目内容
3.若圆中的一条弦和半径相等,则这条弦所对的圆周角为30°或150°.分析 画出图形,利用等边三角形的性质得到∠AOB度数,利用圆周角定理求出弦AB所对的圆周角即可.
解答 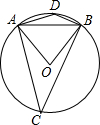 解:如图所示,OA=OB=AB,
解:如图所示,OA=OB=AB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∵∠ACB与∠AOB都对$\widehat{AB}$,
∴∠ACB=$\frac{1}{2}$∠AOB=30°,
∵四边形ACBD为圆O的内角四边形,
∴∠ADB=150°,
若圆中的一条弦和半径相等,则这条弦所对的圆周角为30°或150°,
故答案为:30°或150°
点评 此题考查了圆周角定理,以及等边三角形的判定与性质,熟练掌握圆周角定理是解本题的关键.

练习册系列答案
相关题目
13.九年级数学兴趣小组经过市场调查,得到某种运动服进价为每件60元,每月的销量与售价的相关信息如表:
设该运动服的售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价x(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量y(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
11.下列各式中一定是二次根式的是( )
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{x}$ | C. | $\root{3}{27}$ | D. | $\sqrt{{x}^{2}-2}$ |
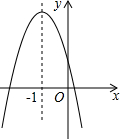 已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )
已知二次函数y=ax2+bx+c的图象如图,以下结论正确的有( )