题目内容
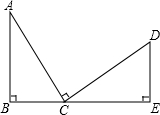如图，B、C、E共线，AB⊥BE，DE⊥BE，AC⊥DC，AC=DC，又AB=2cm，DE=1cm，则BE=考点：全等三角形的判定与性质
专题：常规题型
分析：易证△ABC≌△CED，可得AB=CE，BC=DE，可以求得BE的值．
解答：解：∵AC⊥DC，∴∠ACB+∠ECD=90°
∵AB⊥BE，∴∠ACB+∠A=90°，
∴∠A=∠ECD，
在△ABC和△CED中，
，
∴△ABC≌△CED（AAS），
∴AB=CE=2cm，BC=DE=1cm，
∴BE=BC+CE=3cm．
故答案为3cm．
∵AB⊥BE，∴∠ACB+∠A=90°，
∴∠A=∠ECD，
在△ABC和△CED中，
|
∴△ABC≌△CED（AAS），
∴AB=CE=2cm，BC=DE=1cm，
∴BE=BC+CE=3cm．
故答案为3cm．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ABC≌△CED是解题的关键．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知：如图，AB=DC，AE=BF，CE=DF，∠A=60°．
如图，AB=AC，OB=OC．求证：∠ADC=∠ADB．
已知：如图，AB=DC，AD=BC，O是DB的中点，过O点的直线分别交DA和BC的延长线于E，F．求证：∠E=∠F．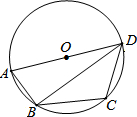
如图，ABCD是⊙O的内接四边形，AD为直径，∠C=130°，则∠ADB的度数为
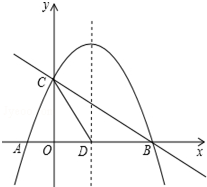如图，抛物线y=-x2+x+2与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D．
如图，AD、AE分别是△ABC的角平分线和高．