题目内容
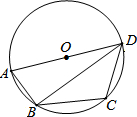 如图,ABCD是⊙O的内接四边形,AD为直径,∠C=130°,则∠ADB的度数为
如图,ABCD是⊙O的内接四边形,AD为直径,∠C=130°,则∠ADB的度数为考点:圆周角定理
专题:
分析:由AD是直径,可得∠ABD=90°,又由ABCD是⊙O的内接四边形,∠C=130°,可求得∠A的度数,根据三角形内角和定理,即可求得答案.
解答:解:∵AD是直径,
∴∠ABD=90°,
又∵ABCD是⊙O的内接四边形,∠C=130°,
∴∠A=180°-130°=50°,
∴∠ADB=180°-90°-50°=40°.
故答案为:40°.
∴∠ABD=90°,
又∵ABCD是⊙O的内接四边形,∠C=130°,
∴∠A=180°-130°=50°,
∴∠ADB=180°-90°-50°=40°.
故答案为:40°.
点评:此题考查了圆周角定理以及弧、弦与圆心角的关系,圆内接四边形的性质.注意掌握数形结合思想的应用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为( )
如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为( )| A、30° | B、40° |
| C、46° | D、60° |
方程y2-y+
=0的两根的情况是( )
| 1 |
| 4 |
| A、没有实数根 |
| B、有两个不相等的实数根 |
| C、有两个相等的实数根 |
| D、不能确定 |
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=36°,则∠3=
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=36°,则∠3=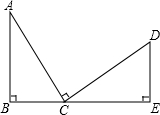 如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE=
如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE= 如图,PA、PB分别和圆O相切于点A、B,点C是
如图,PA、PB分别和圆O相切于点A、B,点C是
