题目内容
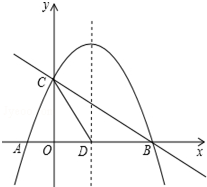 如图,抛物线y=-x2+x+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.
如图,抛物线y=-x2+x+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.(1)求A、B、C、D的坐标;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E(m,n)是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
考点:二次函数综合题
专题:压轴题
分析:(1)令y=0,解关于x的一元二次方程即可得到点A、B的坐标,令x=0,求出y的值,即可得到点C的坐标,求出抛物线对称轴,然后写出点D的坐标;
(2)利用勾股定理求出CD,然后分①点C是顶角顶点时,利用等腰三角形三线合一的性质求解,②点D是顶角顶点时,分点P在点D的上方和下方两种情况写出点P的坐标;
(3)利用待定系数法求一次函数解析式求出直线BC的解析式,表示出EF,再根据S△CBF=S△CBE+S△BEF列式整理,然后根据二次函数的最值问题解答.
(2)利用勾股定理求出CD,然后分①点C是顶角顶点时,利用等腰三角形三线合一的性质求解,②点D是顶角顶点时,分点P在点D的上方和下方两种情况写出点P的坐标;
(3)利用待定系数法求一次函数解析式求出直线BC的解析式,表示出EF,再根据S△CBF=S△CBE+S△BEF列式整理,然后根据二次函数的最值问题解答.
解答:解:(1)令y=0,则-x2+x+2=0,
解得x1=-1,x2=2,
所以,A(-1,0),B(2,0),
令x=0,则y=2,
所以,点C(0,2),
对称轴为直线x=-
=
,
所以,点D(
,0);
(2)由(1)可知,OC=2,OD=
,
所以,CD=
=
,
①点C是顶角顶点时,由等腰三角形三线合一的性质得,点P的纵坐标为点C的2倍,即2×2=4,
所以,点P的坐标为(
,4),
②点D是顶角顶点时,若点P在点D的上方,则P(
,
),
若点P在点D的下方,则P(
,-
);
综上所述,抛物线对称轴上存在点P(
,4)或(
,
)或(
,-
),使△PCD是以CD为腰的等腰三角形;
(3)设直线BC的解析式为y=kx+b,
则
,
解得
,
所以,直线BC的解析式为y=-x+2,
∵点E(m,n)是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
∴EF=-m2+m+2-(-m+2)=-m2+2m,
∴S△CBF=S△CBE+S△BEF,
=
(-m2+2m)×2,
=-m2+2m,
=-(m-1)2+1,
∴当m=1时,△CBF的面积最大为1,
此时,n=-1+2=1,
所以,点E的坐标为(1,1).
解得x1=-1,x2=2,
所以,A(-1,0),B(2,0),
令x=0,则y=2,
所以,点C(0,2),
对称轴为直线x=-
| 1 |
| 2×(-1) |
| 1 |
| 2 |
所以,点D(
| 1 |
| 2 |
(2)由(1)可知,OC=2,OD=
| 1 |
| 2 |
所以,CD=
22+(
|
| ||
| 2 |
①点C是顶角顶点时,由等腰三角形三线合一的性质得,点P的纵坐标为点C的2倍,即2×2=4,
所以,点P的坐标为(
| 1 |
| 2 |
②点D是顶角顶点时,若点P在点D的上方,则P(
| 1 |
| 2 |
| ||
| 2 |
若点P在点D的下方,则P(
| 1 |
| 2 |
| ||
| 2 |
综上所述,抛物线对称轴上存在点P(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(3)设直线BC的解析式为y=kx+b,
则
|

解得
|
所以,直线BC的解析式为y=-x+2,
∵点E(m,n)是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
∴EF=-m2+m+2-(-m+2)=-m2+2m,
∴S△CBF=S△CBE+S△BEF,
=
| 1 |
| 2 |
=-m2+2m,
=-(m-1)2+1,
∴当m=1时,△CBF的面积最大为1,
此时,n=-1+2=1,
所以,点E的坐标为(1,1).
点评:本题是二次函数综合题型,主要利用了二次函数与坐标轴的交点的求解,勾股定理,等腰三角形的性质,三角形的面积,二次函数的最值问题,难点在于(2)分情况讨论,(3)把△CBF的面积的面积分成两个三角形列式整理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程y2-y+
=0的两根的情况是( )
| 1 |
| 4 |
| A、没有实数根 |
| B、有两个不相等的实数根 |
| C、有两个相等的实数根 |
| D、不能确定 |
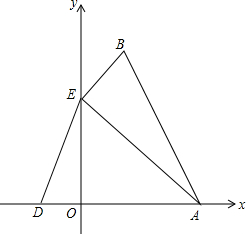 顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.
顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.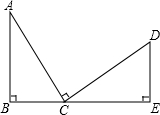 如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE=
如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE=
 如图,PA、PB分别和圆O相切于点A、B,点C是
如图,PA、PB分别和圆O相切于点A、B,点C是
 如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是
如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是