题目内容
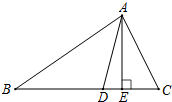 如图,AD、AE分别是△ABC的角平分线和高.
如图,AD、AE分别是△ABC的角平分线和高.(1)若已知△ABC是直角三角形,∠B=20°,∠C=70°,则∠DAE=
(2)若已知∠B=25°,∠C=85°,则∠DAE=
(3)若已知∠B=α,∠C=β,且,求∠DAE的度数(结果用含α、β的代数式表示).
考点:三角形的角平分线、中线和高,三角形内角和定理,三角形的外角性质
专题:
分析:(1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=90°,再根据角平分线与高线的定义得到∠CAD=
∠CAB=45°,∠AEC=90°,则∠CAE=90°-∠C=20°,然后利用∠DAE=∠CAD-∠CAE计算即可.
(2)先根据三角形内角和得到∠CAB=180°-∠B-∠C=70°,再根据角平分线与高线的定义得到∠CAD=
∠CAB=35°,∠AEC=90°,则∠CAE=90°-∠C=5°,然后利用∠DAE=∠CAD-∠CAE计算即可.
(3)先根据三角形内角和得到∠CAB=180°-α-β,再根据角平分线与高线的定义得到∠DAC=90°-
α-
β,∠AEC=90°,则∠CAE=90°-∠C=90°-β,然后利用∠DAE=∠CAD-∠CAE计算即可.
| 1 |
| 2 |
(2)先根据三角形内角和得到∠CAB=180°-∠B-∠C=70°,再根据角平分线与高线的定义得到∠CAD=
| 1 |
| 2 |
(3)先根据三角形内角和得到∠CAB=180°-α-β,再根据角平分线与高线的定义得到∠DAC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵∠B=20°,∠C=70°,
∴∠BAC=90°,
∴∠DAC=45°,
∵AE是△ABC的高.
∴∠EAC=20°,
∴∠DAE=45°-20°=25°;
(2)∵∠B=25°,∠C=85°
∴∠BAC=70°,
∵AD是△ABC的角平分线,
∴∠DAC=35°,
∵AE是△ABC的高.
∴∠EAC=5°,
∴∠DAE=35°-5°=30°;
(3)在△ABC中,∠BAC=180°-α-β,
∵AD是△ABC的角平分线,
∴∠DAC=90°-
α-
β,
∵AE是△ABC的高.
∴∠EAC=90°-β,
∴∠DAE=∠DAC-∠EAC=90°-
α-
β-90°+β=
(α-β),
故答案为25°,30°.
∴∠BAC=90°,
∴∠DAC=45°,
∵AE是△ABC的高.
∴∠EAC=20°,
∴∠DAE=45°-20°=25°;
(2)∵∠B=25°,∠C=85°
∴∠BAC=70°,
∵AD是△ABC的角平分线,
∴∠DAC=35°,
∵AE是△ABC的高.
∴∠EAC=5°,
∴∠DAE=35°-5°=30°;
(3)在△ABC中,∠BAC=180°-α-β,
∵AD是△ABC的角平分线,
∴∠DAC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∵AE是△ABC的高.
∴∠EAC=90°-β,
∴∠DAE=∠DAC-∠EAC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为25°,30°.
点评:本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
下列函数是二次函数的是( )
| A、y=x+1 | ||
| B、y=5x2+1 | ||
C、y=3x2+
| ||
D、y=
|
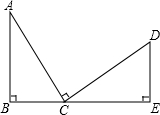 如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE=
如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE= 如图,PA、PB分别和圆O相切于点A、B,点C是
如图,PA、PB分别和圆O相切于点A、B,点C是
 如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是
如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是
 如图,已知点B的坐标为(6,0),点P的坐标为(4,-4),在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,已知点B的坐标为(6,0),点P的坐标为(4,-4),在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由.