题目内容
已知AB是⊙O的弦,EF切⊙O于B,AC⊥EF于C,求证:AB2=2AC•AO.
考点:切线的性质
专题:证明题
分析:如图,作直径AD,连结OB、BD,先根据切线的性质得OB⊥AC,加上AC⊥EF,则OB∥AC,根据平行线的性质得∠2=∠3,易得∠1=∠2,再根据圆中由AD为直径得到∠ABD=90°,于是可证得Rt△ABD∽Rt△ACB,利用相似比得AB2=AC•AD,再把AD=2AO代入即可得到结论.
解答:证明:如图, 作直径AD,连结OB、BD,
作直径AD,连结OB、BD,
∵EF切⊙O于B,
∴OB⊥AC,
∵AC⊥EF,
∴OB∥AC,
∴∠2=∠3,
∵OA=OB,
∴∠1=∠3,
∴∠1=∠2,
∵AD为直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△ACB,
∴
=
,
∴AB2=AC•AD,
而AD=2AO,
∴AB2=2AC•AO.
 作直径AD,连结OB、BD,
作直径AD,连结OB、BD,∵EF切⊙O于B,
∴OB⊥AC,
∵AC⊥EF,
∴OB∥AC,
∴∠2=∠3,
∵OA=OB,
∴∠1=∠3,
∴∠1=∠2,
∵AD为直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△ACB,
∴
| AB |
| AC |
| AD |
| AB |
∴AB2=AC•AD,
而AD=2AO,
∴AB2=2AC•AO.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和相似三角形的判定与性质.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
若(a-1)2+|b+2|=0,则(a+b)2014的值是( )
| A、-1 | B、1 | C、0 | D、2014 |
下列计算正确的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
下列函数是二次函数的是( )
| A、y=x+1 | ||
| B、y=5x2+1 | ||
C、y=3x2+
| ||
D、y=
|
 如图,已知:∠E=∠F,∠B=∠C,AE=AF,试说明:(1)△ABE≌△ACF;(2)BM=CN.
如图,已知:∠E=∠F,∠B=∠C,AE=AF,试说明:(1)△ABE≌△ACF;(2)BM=CN.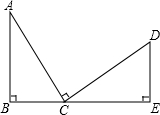 如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE=
如图,B、C、E共线,AB⊥BE,DE⊥BE,AC⊥DC,AC=DC,又AB=2cm,DE=1cm,则BE= 如图,⊙O的半径OC⊥AB,垂足为E,若∠B=28°,则∠A的度数为
如图,⊙O的半径OC⊥AB,垂足为E,若∠B=28°,则∠A的度数为