题目内容
5.(x2-1)2-5(x2-1)+4=0x2-1=y
∴y2-5y+4=0
∴y1=1,y2=4
当y1=1时,x2-1=0∴x2=2,∴x=±$\sqrt{2}$
当y2=4时,x2-1=4∴x2=5,∴x=±$\sqrt{5}$
∴x=±$\sqrt{2}$,±$\sqrt{5}$
用同种方法解x4-x2-6=0.
分析 设x2=y,则原方程化为y2-y-6=0,求出y的值,代入求出x即可.
解答 解:x4-x2-6=0,
设x2=y,则原方程化为:y2-y-6=0,
解得:y1=3,y2=-2,
当y1=3时,x2=3,
解得:x1=$\sqrt{3}$,x2=-$\sqrt{3}$;
当y2=-2时,x2=-2,
此方程无解;
所以原方程的解为:x1=$\sqrt{3}$,x2=-$\sqrt{3}$.
点评 本题考查了用换元法解一元二次方程的应用,能正确换元是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,在下列条件中,一定能得到AB∥CD是( )
如图,在下列条件中,一定能得到AB∥CD是( )
 如图,在下列条件中,一定能得到AB∥CD是( )
如图,在下列条件中,一定能得到AB∥CD是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠5=∠6 | D. | ∠7=∠8 |
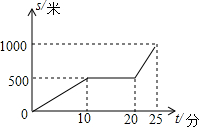 某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,如图是王老师从家到学校这一过程中的所有路程s(米)与时间t(分)之间的关系.
某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,如图是王老师从家到学校这一过程中的所有路程s(米)与时间t(分)之间的关系. 如图,已知△ABC中,AD是△ABC外角∠EAC的平分线且交BC的延长线于点D,比较∠ACB与∠B的大小,并说出理由.
如图,已知△ABC中,AD是△ABC外角∠EAC的平分线且交BC的延长线于点D,比较∠ACB与∠B的大小,并说出理由. 如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.
如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.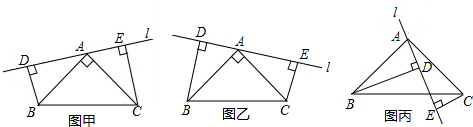
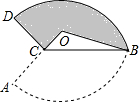 如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.
如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.