题目内容
5.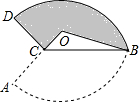 如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.
如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.
分析 过点B作BE⊥AO,垂足为E,作点O关于BC的对称点O′,在Rt△OBE和Rt△CBE中,求得EB、OE的长,从而得到OC的长,最后根据S扇DO′B-2S△COB进行计算即可.
解答 解:如图所示,过点B作BE⊥AO,垂足为E,作点O关于BC的对称点O′.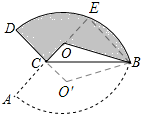
∵∠DCA=90°,
∴∠ECO′=90°.
由翻折的性质可知:∠OAB=∠O′CB=45°.
∴CE=EB.
∵∠AOB=120°,
∴∠EOB=60°.
∴∠OBE=30°.
∴OE=$\frac{1}{2}OB=\frac{1}{2}×2\sqrt{3}=\sqrt{3}$.
∴$\frac{BE}{OB}=\frac{\sqrt{3}}{2}$,即$\frac{EB}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$.
解得:BE=3.
∴CE=3.
∴OC=3-$\sqrt{3}$.
阴影部分的面积=S扇DO′B-2S△COB=$\frac{120°π×(2\sqrt{3})^{2}}{360°}$-2×$\frac{1}{2}$×$(3-\sqrt{3})×3$=4$π+3\sqrt{3}-9$.
故答案为:4$π+3\sqrt{3}-9$.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数值、扇形的面积,将不规则图形面积转化为规则图形的面积进行计算是解题的关键.

练习册系列答案
相关题目
15.下列计算错误的是( )
| A. | -12x4÷3x=-4x3 | B. | 2x2+3x2=5x2 | C. | $\sqrt{8}=2\sqrt{2}$ | D. | (x2)3=x5 |
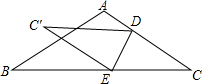 如图,把三角形纸片ABC沿DE折叠,∠ADC′=30°,∠BEC′=40°,求∠C′的度数.
如图,把三角形纸片ABC沿DE折叠,∠ADC′=30°,∠BEC′=40°,求∠C′的度数.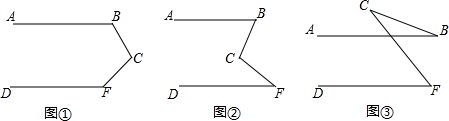
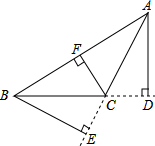 如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段BE是△ABC中AC边上的高.
如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段BE是△ABC中AC边上的高.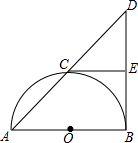 如图,AB是半圆O的直径,EB、EC分别与半圆O相切于点B、C,连接AC并延长,与BE的延长线交于点D.
如图,AB是半圆O的直径,EB、EC分别与半圆O相切于点B、C,连接AC并延长,与BE的延长线交于点D.