题目内容
2.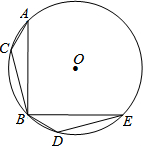 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 连接OC、OB、OD,根据圆周角定理求出∠BOC=60°,得到△OCB是等边三角形,求出OC=OB=BC=$\sqrt{2}$,根据旋转的性质得到∠COD=90°,根据勾股定理计算即可.
解答 解: 连接OC、OB、OD,
连接OC、OB、OD,
由圆周角定理得,∠BOC=2∠A=60°,
∴△OCB是等边三角形,
∴OC=OB=BC=$\sqrt{2}$,
由旋转的性质可知,∠COD=90°,
∴CD=$\sqrt{O{C}^{2}+O{B}^{2}}$=2,
故选:D.
点评 本题考查的是三角形的外接圆与外心的概念和性质,掌握圆周角定理、勾股定理、等边三角形的判定定理是解题的关键.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | (a+2)2=a2+4 | B. | x3+x2=x5 | C. | $\frac{2}{2x+y}$=$\frac{1}{x+y}$ | D. | (-3a3)2=9a6 |
17. 已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
 已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )| A. | a<-1 | B. | a>-1 | C. | a≤-1 | D. | a≥-1 |
7.a,b,c为△ABC的三边,化简|a+b+c|-|a-b-c|的结果( )
| A. | 2b+2c | B. | 2b-2c | C. | 0 | D. | 2a |
11.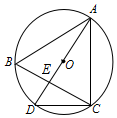 如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )
如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )
 如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )
如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )| A. | 4 | B. | $\frac{21}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
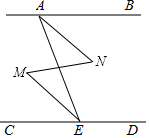 如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.
如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.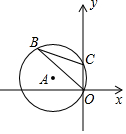 如图,半径为3的⊙A经过原点O和点C(0,2),B是⊙O上一点,则tan∠OBC为$\frac{\sqrt{2}}{4}$.
如图,半径为3的⊙A经过原点O和点C(0,2),B是⊙O上一点,则tan∠OBC为$\frac{\sqrt{2}}{4}$.