题目内容
11.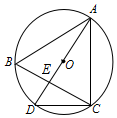 如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )
如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )| A. | 4 | B. | $\frac{21}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 根据勾股定理求出CD,证明△AEC∽△ACD,根据相似三角形的性质列出比例式,计算即可.
解答 解:∵⊙O的半径为5,DE=3,
∴AE=10-3=7,
∵AD是直径,
∴∠ACD=90°,
∴CD=6,
∵AB=AC,
∴∠ACE=∠D,又∠DAC=∠CAE,
∴△AEC∽△ACD,
∴$\frac{AE}{AC}$=$\frac{EC}{CD}$,即$\frac{7}{8}$=$\frac{EC}{6}$,
解得,EC=$\frac{21}{4}$,
故选:B.
点评 本题考查的是三角形的外接圆与外心的概念和性质,掌握圆周角定理、相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
1.“3.15“植树节活动后,某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分;
表1:栽下的各品种树苗棵数统计表表
请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.
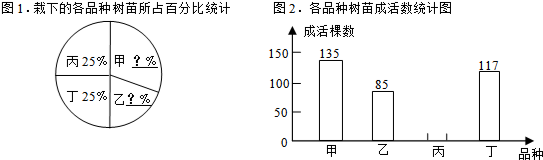
表1:栽下的各品种树苗棵数统计表表
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 |
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.

2.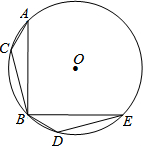 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
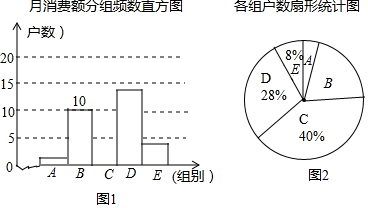
19.在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.我市区机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题:
月消费额分组统计表
(1)A组的频数是2,本次调查样本的容量是50;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额少于300元的户数是多少?

月消费额分组统计表
| 组别 | 消费额(x)元 |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额少于300元的户数是多少?
16. 实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
 实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )| A. | a | B. | b | C. | -b | D. | c |
3.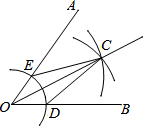 用尺规作图法作已知角∠AOB的平分线的步骤如下:
用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
 用尺规作图法作已知角∠AOB的平分线的步骤如下:
用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
10.下列计算正确的是( )
| A. | (ab)3=a3b | B. | $\frac{{a}^{6}}{{a}^{2}}$=a3 | C. | $\frac{-a-b}{a+b}$=-1 | D. | (a+b)2=a2+b2 |
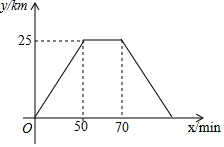 甲、乙两人分别从A、B两地同时出发,匀速骑行,甲到达B地停留一段时间后以原速返回A地,乙到达A地后停止骑行.图中的折线表示甲离A地的路程y(km)与所用时间x(min)的函数关系.
甲、乙两人分别从A、B两地同时出发,匀速骑行,甲到达B地停留一段时间后以原速返回A地,乙到达A地后停止骑行.图中的折线表示甲离A地的路程y(km)与所用时间x(min)的函数关系. 如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m2,则地面上的阴影面积是2.7m2.
如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m2,则地面上的阴影面积是2.7m2.