题目内容
13.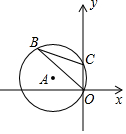 如图,半径为3的⊙A经过原点O和点C(0,2),B是⊙O上一点,则tan∠OBC为$\frac{\sqrt{2}}{4}$.
如图,半径为3的⊙A经过原点O和点C(0,2),B是⊙O上一点,则tan∠OBC为$\frac{\sqrt{2}}{4}$.
分析 作直径CD,根据勾股定理求出OD,根据正切的定义求出tan∠CDO,根据圆周角定理得到∠OBC=∠CDO,等量代换即可.
解答 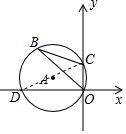 解:作直径CD,
解:作直径CD,
在Rt△OCD中,CD=6,OC=2,
则OD=$\sqrt{C{D}^{2}-O{C}^{2}}$=4$\sqrt{2}$,
tan∠CDO=$\frac{OC}{OD}$=$\frac{\sqrt{2}}{4}$,
由圆周角定理得,∠OBC=∠CDO,
则tan∠OBC=$\frac{\sqrt{2}}{4}$,
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查的是圆周角定理、锐角三角函数的定义,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.“3.15“植树节活动后,某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分;
表1:栽下的各品种树苗棵数统计表表
请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.
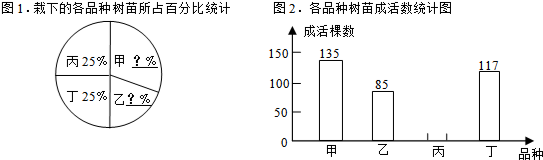
表1:栽下的各品种树苗棵数统计表表
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 |
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.

2.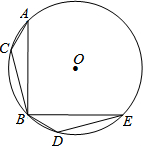 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.
如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.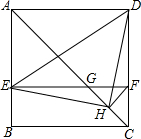 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论: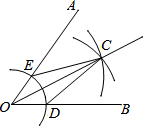 用尺规作图法作已知角∠AOB的平分线的步骤如下:
用尺规作图法作已知角∠AOB的平分线的步骤如下: