题目内容
4.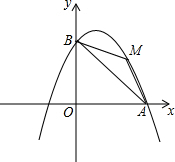 如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.
如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.(1)求该抛物线的解析式及其顶点C的坐标;
(2)若点M是抛物线上的一个动点,且位于第一象限内.
①设△ABM的面积为S,试求S的最大值;
②若S为整数,则这样的M点有7个.
分析 (1)先利用抛物线的对称性确定抛物线与x轴的另一个交点坐标,再设交点式y=a(x+2)(x-4),然后把C点坐标代入求出a即可得到抛物线的解析式,再把解析式配成顶点式可得C的坐标;
(2)①过M点作MN∥y轴交AB于N点,如图,利用待定系数法求出直线AB的解析式,则可设M(t,-$\frac{1}{2}$t2+t+4),则N(t,-t+4),于是用t可表示出MN,再利用S=S△BMN+S△AMN=$\frac{1}{2}$•4•MN得到S与m的二次函数,然后根据二次函数的性质求解;
②利用S的整数值可为1、2、3、4,则计算出对应的t的值,从而可判断M点的个数.
解答 解:(1)∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点为A(4,0),
∴抛物线与x轴的另一个交点为(-2,0),
设抛物线的解析式为y=a(x+2)(x-4),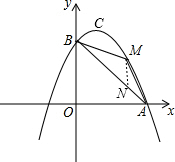
把B(0,4)代入得a•2•(-4)=4,解得a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$(x+2)(x-4),即y=-$\frac{1}{2}$x2+x+4;
∵y=-$\frac{1}{2}$(x-1)2+$\frac{9}{2}$,
∴抛物线的顶点C的坐标为(1,$\frac{9}{2}$);
(2)①过M点作MN∥y轴交AB于N点,如图,
设AB的解析式为y=mx+n,把B(0,4)、A(4,0)代入得$\left\{\begin{array}{l}{n=4}\\{4m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=4}\end{array}\right.$,
∴直线AB的解析式为y=-x+4,
设M(t,-$\frac{1}{2}$t2+t+4),则N(t,-t+4),
∴MN=-$\frac{1}{2}$t2+t+4-(-t+4)=-$\frac{1}{2}$t2+2t,
∴S=S△BMN+S△AMN=$\frac{1}{2}$•4•MN=$\frac{1}{2}$•4•(-$\frac{1}{2}$t2+2t)=-t2+4t=-(t-2)2+4,
∴当t=2时,S有最大值,最大值为4;
②∵S的最大值为4,
∴S的整数值可为1、2、3、4,
当S=1时,-(t-2)2+4=1,解得t=2±$\sqrt{3}$,
当S=2时,-(t-2)2+4=2,解得t=2±$\sqrt{2}$,
当S=3时,-(t-2)2+4=3,解得t=1或3,
当S=4时,-(t-2)2+4=4,解得t=2,
∴这样的M点有7个.
故答案为7.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;理解坐标与图形性质.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | 2m | B. | 3m | C. | 4m | D. | 5m |
| A. | 在1和2之间 | B. | 在2和3之间 | C. | 在3和4之间 | D. | 在4和5之间 |
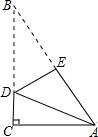 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
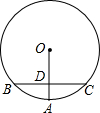 如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8. 如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;
如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;