题目内容
4.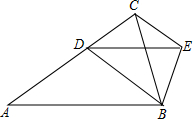 如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;
如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;(1)联结CE,求证:CE=BE;
(2)分别延长CE、AB交于点F,求证:四边形DBFE是菱形.
分析 (1)根据等边对等角,计算出∠4,∠2,∠3的度数为36°,然后再证明CO=EO,进而可得∠5=36°,再根据等角对等边可得CE=BE;
(2)首先根据内错角相等,两直线平行证明DE∥BF,DB∥BC,进而可得四边形DBFE是平行四边形,再根据邻边相等的平行四边形是菱形可得结论.
解答 证明:(1)∵AB=AC,
∴∠ACB=∠ABC=72°,
∴∠A=180°-72°-72°=36°,
∵AD=BD,
∴∠1=∠A=36°,
∴∠2=36°,
∵∠DBE=72°,
∴∠3=36°,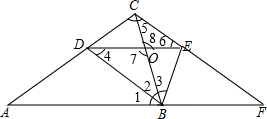
∵BD=DE,
∴∠DEB=∠DBE=72°,
∴∠BOE=180°-∠3-∠DEB=72°,
∴∠4=∠BOE-∠2=36°,
∴∠2=∠4,
∴DO=BO,
∵∠2=36°,∠ACB=72°,
∴∠BDC=180°-∠2-∠DCB=72°,
∴BC=BD,
∵BD=DE,
∴BC=DE,
∴DE-DO=BC-BO,
∴CO=EO,
∵∠7=∠8,
∴∠5=∠$\frac{180°-∠8}{2}$=$\frac{180°-∠7}{2}$=∠4=36°,
∴∠5=∠3=36°,
∴CE=BE;
(2)∵∠4=∠1=36°,
∴DE∥BF,
∵∠2=∠5=36°,
∴EF∥DB,
∴四边形DEFB是平行四边形,
∵DE=DB,
∴四边形DBFE是菱形.
点评 此题主要考查了等腰三角形的性质和判定,以及菱形的判定,关键是掌握等边对等角,推出∠5=∠3=36°.

练习册系列答案
相关题目
19.为了了解某区5500名初三学生的体重情况,随机抽测了400名学生的体重,统计结果列表如下:
那么样本中体重在50-55范围内的频率是0.21.
| 体重(千克) | 频数 | 频率 |
| 40-45 | 44 | |
| 45-50 | 66 | |
| 50-55 | 84 | |
| 55-60 | 86 | |
| 60-65 | 72 | |
| 65-70 | 48 |
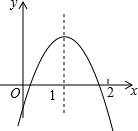 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论: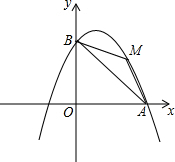 如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.
如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.
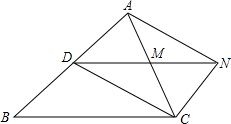 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.