题目内容
2.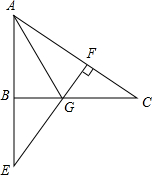 如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.
如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.(1)求证:AG平分∠BAC;
(2)若∠E=40°,求∠AGB的度数.
分析 (1)首先证明△ABC≌△AFE,推出AB=AF,再证明Rt△AGF≌Rt△AGB,推出∠GAF=∠GAB,即可解决问题.
(2)在Rt△BEG中,∠BGE=90°-∠E=50°,推出∠BGF=130°,由Rt△AGF≌Rt△AGB,推出∠AGB=∠AGF=$\frac{1}{2}$∠BGF即可解决问题.
解答 (1)证明:∵EF⊥AC,
∴∠ABC=∠AFE=90°,
在△ABC和△AFE中,
$\left\{\begin{array}{l}{∠BAC=∠EAF}\\{∠ABC=∠AFE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△AFE,
∴AB=AF,
在Rt△AGF和Rt△AGB中,
$\left\{\begin{array}{l}{AG=AG}\\{AF=AB}\end{array}\right.$,
∴Rt△AGF≌Rt△AGB,
∴∠GAF=∠GAB,
∴AG平分∠BAC.
(2)在Rt△BEG中,∠BGE=90°-∠E=50°,
∴∠BGF=130°,
∵Rt△AGF≌Rt△AGB,
∴∠AGB=∠AGF=$\frac{1}{2}$∠BGF=65°.
点评 本题考查全等三角形的判定和性质、直角三角形的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
20.在平面直角坐标系中,已知点P的坐标是(3,4),点P与点Q关于y轴对称,则点Q的坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
10.小明用100元钱购得笔记本和笔共30件,已知每本笔记本2元,每支笔5元,那么小明最多能买笔的数目为
( )
( )
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
 如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.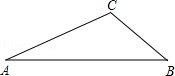 已知△ABC中,∠A=30°,AC=6.
已知△ABC中,∠A=30°,AC=6.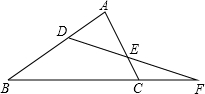 如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°.
如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°. 如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.
如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.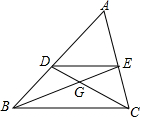 如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.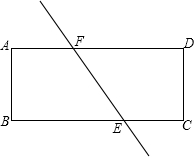 如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.
如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.