题目内容
12．把一张矩形的纸片对折后和原矩形相似，那么大矩形与小矩形的相似比是（ ）| A． | $\sqrt{2}$：1 | B． | 4：1 | C． | 3：1 | D． | 2：1 |
分析 设原矩形的长为2a，宽为b，表示出对折后的矩形的宽为a，然后根据相似多边形对应边成比例列出比例式，即可得出大矩形与小矩形的相似比．
解答 
解：设原矩形的长为2a，宽为b，
则对折后的矩形的长为b，宽为a，
∵对折后所得的矩形与原矩形相似，
∴$\frac{2a}{b}$=$\frac{b}{a}$，
∴大矩形与小矩形的相似比是$\sqrt{2}$：1；
故选A．
点评 本题考查的是相似多边形的性质、矩形的性质，掌握相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
10．用a、3、8和12这四个数组成比例，a可能是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
3．一个底面是正方形的长方体，高为8cm，底面正方形边长为6cm，如果它的高不变，底面正方形的边长减少acm，那么它的体积减少了（ ）
| A． | 96a-8a2 | B． | 8a2-96a | C． | 98a-6a2 | D． | 6a2-98a |
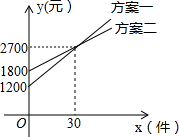某公司推销一种产品，公司付给推销员的月报销有两种方案如图所示．设推销员推销产品的数量为x（件），付给推销员的月报酬为y（元）．若公司决定改进“方案二”，保持基本工资不变，每件报酬增加m元，使得当销售员销售产品达到40件时，两种方案的报酬差额不超过100元，则m的取值范围是2.5≤m≤7.5．
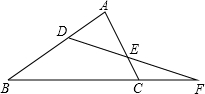如图所示，∠B=67°，∠ACB=74°，∠AED=48°，则∠BDF=87°．
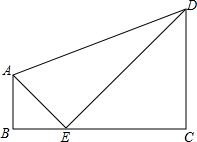如图，已知直角梯形ABCD中，∠ABC=∠DCB=90°，点E在高上，且BE=AB=a，CE=CD=b，
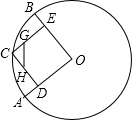在⊙O中，半径OA、OB互相垂直，点C为弧$\widehat{AB}$上一点（不与A、B重合），CD⊥OA，CE⊥OB，垂足分别为D、E．点G、H分别在CE、CD上，且CG=$\frac{1}{3}$CE，CH=$\frac{1}{3}$CD，当C点在弧$\widehat{AB}$上运动时，GH的长度（ ）
如图点P和P1关于直线n轴对称，点P和P2关于直线m轴对称，连结P1P2交m于点A，交n于点B，连结PA和PB，若△PAB的周长为10，则P1P2=10．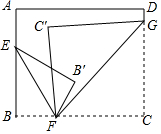
如图所示．将一张长方形纸片分别沿着EF，FG对折，使点B落在点B′，点C落在C′（B′在C′的右侧），若∠B′FC′=28°，则∠EFG的度数为104°．