题目内容
19.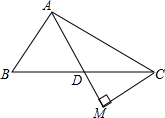 在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)
在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)
分析 延长AM到E,使ME=AM,连接CE,求出AC=CE,求出DE=EC,即可得出答案.
解答 证明:延长AM到E,使ME=AM,连接CE,
则AE=2AM,
∵CM⊥AE,
∴AC=CE,
∴∠E=∠CAD=∠DAB,
∴AB∥EC,
∴∠B=∠ECD,
∵AB=AD,
∴∠B=∠ADB,
∵∠ADB=∠EDC,
∴∠ECD=∠EDC,
∴EC=ED,
∴AE=2AM=AD+ED=AB+AC.
∴AM=$\frac{1}{2}$(AB+CA).
点评 本题考查了平行线的性质和判定,线段垂直平分线性质,等腰三角形的性质和判定的应用,解此题的关键是推出DE=EC,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
10.小明用100元钱购得笔记本和笔共30件,已知每本笔记本2元,每支笔5元,那么小明最多能买笔的数目为
( )
( )
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
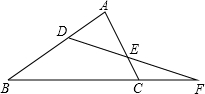 如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°.
如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°. 如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.
如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.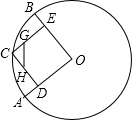 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )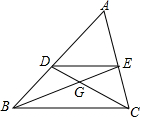 如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.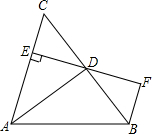 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.