题目内容
6.分式$\frac{7}{x-2}$与$\frac{x}{2-x}$的和为4,则x的值为3.分析 首先根据分式$\frac{7}{x-2}$与$\frac{x}{2-x}$的和为4,可得:$\frac{7}{x-2}$+$\frac{x}{2-x}$=4,然后根据解分式方程的方法,求出x的值为多少即可.
解答 解:∵分式$\frac{7}{x-2}$与$\frac{x}{2-x}$的和为4,
∴$\frac{7}{x-2}$+$\frac{x}{2-x}$=4,
去分母,可得:7-x=4x-8
解得:x=3
经检验x=3是原方程的解,
∴x的值为3.
故答案为:3.
点评 此题主要考查了解分式方程问题,要熟练掌握,解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

练习册系列答案
相关题目
1.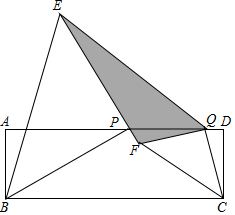 如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )
如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )
 如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )
如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
18.已知抛物线y=x2+bx+c的对称轴为x=1.且与x轴交于A、B两点,AB=2.若关于x的一元二次方程x2+bx+c=t(t为实数)在-2≤x<$\frac{7}{2}$的范围囤内有实数解.t的取值范围是( )
| A. | 1≤t≤$\frac{21}{4}$ | B. | -2≤t≤3 | C. | -1≤t<8 | D. | -2≤t<8 |
15.下列计算正确的是( )
| A. | 3x4-x2=3x2 | B. | (-2ab3)2•a=4a3b6 | C. | 8a6÷2a3=4a2 | D. | (a-2)2=a2-4 |
 如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.

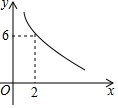 平行四边形ABCD中,AB⊥AC,∠B=45°.若平行四边形ABCD的一边长x与这条边上的高为y满足的反比例函数关系如图所示,则平行四边形ABCD的周长为4($\sqrt{3}$+$\sqrt{6}$).
平行四边形ABCD中,AB⊥AC,∠B=45°.若平行四边形ABCD的一边长x与这条边上的高为y满足的反比例函数关系如图所示,则平行四边形ABCD的周长为4($\sqrt{3}$+$\sqrt{6}$). 如图,A、B、C是⊙O上的三点,且四边形OABC是菱形.若点D是圆上异于A、B、C的另一点,则∠ADC的度数是60°或120°.
如图,A、B、C是⊙O上的三点,且四边形OABC是菱形.若点D是圆上异于A、B、C的另一点,则∠ADC的度数是60°或120°.