题目内容
1.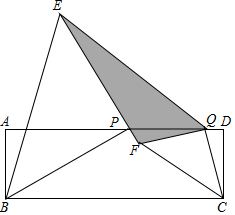 如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )
如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 先过E作EG⊥AD于G,作FH⊥AD于H,依据△QFH≌△CQD,可得FH=DQ;依据△EGP≌△APB,可得EG=AP,再根据AP+DQ=4,即可得出EG+FH=4,最后根据阴影部分的面积=$\frac{1}{2}$PQ×EG+$\frac{1}{2}$PQ×FH=$\frac{1}{2}$PQ×(EG+FH),进行计算即可.
解答 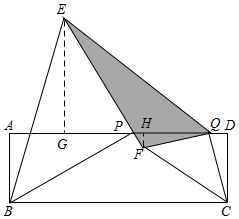 解:如图所示,过E作EG⊥AD于G,作FH⊥AD于H,
解:如图所示,过E作EG⊥AD于G,作FH⊥AD于H,
∵△CFQ是等腰直角三角形,∠D=90°,
∴∠QHF=∠CDQ=90°,QF=CQ,∠FQH=∠QCD,
∴△QFH≌△CQD,
∴FH=DQ,
∵△BEP是等腰直角三角形,∠A=90°,
∴∠EGP=∠A=90°,EP=PB,∠GEP=∠APB,
∴△EGP≌△APB,
∴EG=AP,
又∵BC=6=AD,PQ=2,
∴AP+DQ=6-2=4,
∴EG+FH=4,
∴阴影部分的面积=△EPQ的面积+△FPQ的面积
=$\frac{1}{2}$PQ×EG+$\frac{1}{2}$PQ×FH
=$\frac{1}{2}$PQ×(EG+FH)
=$\frac{1}{2}$×2×4
=4,
故选:B.
点评 本题主要考查了矩形的性质,全等三角形的判定与性质以及等腰直角三角形的性质的运用,解决问题的关键是利用等腰直角三角形,作辅助线构造全等三角形,依据全等三角形的对应边相等进行推导计算.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
9.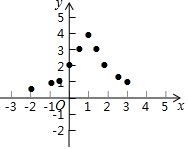 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{4}{{(x-1)}^{2}+1}$的自变量x的取值范围是全体实数;
(2)表格是y与x的几组对应值.
表中m的值为$\frac{2}{5}$;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
根据描出的点,画出函数y=$\frac{4}{{(x-1)}^{2}+1}$的大致图象;
(4)结合函数图象,请写出函数y=$\frac{4}{{(x-1)}^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)如果方程$\frac{4}{{(x-1)}^{2}+1}$=a有2个解,那么a的取值范围是0<a<4.
 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:(1)函数y=$\frac{4}{{(x-1)}^{2}+1}$的自变量x的取值范围是全体实数;
(2)表格是y与x的几组对应值.
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{3}$ | m | … |
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
根据描出的点,画出函数y=$\frac{4}{{(x-1)}^{2}+1}$的大致图象;
(4)结合函数图象,请写出函数y=$\frac{4}{{(x-1)}^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)如果方程$\frac{4}{{(x-1)}^{2}+1}$=a有2个解,那么a的取值范围是0<a<4.
13.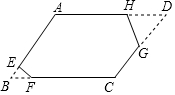 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
10.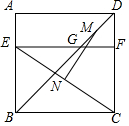 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 4 |

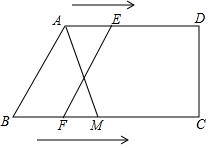 在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
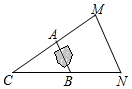 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.
如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.