题目内容
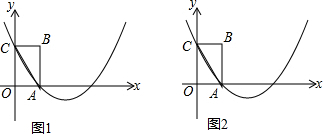
18.已知抛物线y=x2+bx+c的对称轴为x=1.且与x轴交于A、B两点,AB=2.若关于x的一元二次方程x2+bx+c=t(t为实数)在-2≤x<$\frac{7}{2}$的范围囤内有实数解.t的取值范围是( )| A. | 1≤t≤$\frac{21}{4}$ | B. | -2≤t≤3 | C. | -1≤t<8 | D. | -2≤t<8 |
分析 利用二次函数y=x2+bx+c的对称轴为直线x=1,且图象与x轴交于A、B两点,AB=2,可求b的值,再利用抛物线的对称性可求A、B两点的坐标,从而可求c,那么关于x的一元二次方程x2+bx+c-t=0(t为实数)可化为x2-2x-t=0,利用公式法求出x,结合-2<x<$\frac{7}{2}$的范围内有实数解,可求出相应的x的取值范围.
解答 解:∵二次函数y=x2+bx+c的对称轴为直线x=1,
∴-$\frac{b}{2}$=1,
解得:b=-2,
∵对称轴为直线x=1,且图象与x轴交于A、B两点,AB=2,
∴直线与x轴交于(2,0),(0,0),
∴当x=0时,0+0+c=0,
∴c=0,
∴关于x的一元二次方程x2+bx+c-t=0(t为实数)为x2-2x-t=0,
∴△=b2-4ac=4+4t≥0,
解得t≥-1,
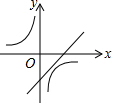
方程x2+bx+c-t=0(t为实数),在-2<x<$\frac{7}{2}$的范围内有实数解可以理解为二次函数y1=x2-2x与直线y2=t有交点,
当x=-2时,y1=8;当x=$\frac{7}{2}$时,y2=$\frac{21}{4}$,
如图所示,
当-1≤t<$\frac{21}{4}$时二次函数y1=x2-2x与直线y2=t有两个交点,
当-1≤t<8时二次函数y1=x2-2x与直线y2=t有一个交点,
因此-1≤t<8即可保证二次函数y1=x2-2x与直线y2=t有交点,
故选C.
点评 本题考查了二次函数的图象与横轴的交点问题、以及抛物线的对称问题.解决本题的关键是正确的理解并应用抛物线与横轴的交点横坐标就是方程的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.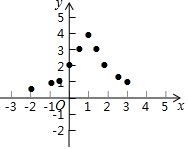 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{4}{{(x-1)}^{2}+1}$的自变量x的取值范围是全体实数;
(2)表格是y与x的几组对应值.
表中m的值为$\frac{2}{5}$;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
根据描出的点,画出函数y=$\frac{4}{{(x-1)}^{2}+1}$的大致图象;
(4)结合函数图象,请写出函数y=$\frac{4}{{(x-1)}^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)如果方程$\frac{4}{{(x-1)}^{2}+1}$=a有2个解,那么a的取值范围是0<a<4.
 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:(1)函数y=$\frac{4}{{(x-1)}^{2}+1}$的自变量x的取值范围是全体实数;
(2)表格是y与x的几组对应值.
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{3}$ | m | … |
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
根据描出的点,画出函数y=$\frac{4}{{(x-1)}^{2}+1}$的大致图象;
(4)结合函数图象,请写出函数y=$\frac{4}{{(x-1)}^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)如果方程$\frac{4}{{(x-1)}^{2}+1}$=a有2个解,那么a的取值范围是0<a<4.
13.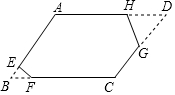 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
10.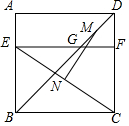 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 4 |

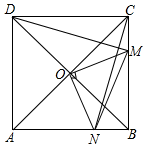 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是$\frac{1}{2}$,其中正确结论的个数是( )
如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是$\frac{1}{2}$,其中正确结论的个数是( )