题目内容
13.计算$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{48}$的结果是( )| A. | 1 | B. | -1 | C. | -$\sqrt{3}$-$\sqrt{2}$ | D. | $\sqrt{2}$-$\sqrt{3}$ |
分析 首先把二次根式化简,然后再合并同类二次根式即可.
解答 解:原式=3$\sqrt{3}$-$\sqrt{2}$-4$\sqrt{3}$=$-\sqrt{3}$$-\sqrt{2}$,
故选:C.
点评 此题主要考查了二次根式的加减,关键是掌握二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.

练习册系列答案
相关题目
11.从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟.根据以上条件,下列说法不正确的是( )
| A. | 设上坡路长x千米,可列方程$\frac{x}{3}-\frac{x}{5}=\frac{54}{60}-\frac{42}{60}$ | |
| B. | 设上坡路长x千米,平路长y千米,可列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$ | |
| C. | 列算式(54-42)÷(5-3)即可求出上坡路长. | |
| D. | 根据条件,能求出甲地到乙地的全程是3.1千米. |
1. 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )
 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )| A. | ∠B=∠ACB | B. | ∠A=∠ACE | C. | ∠B=∠ACE | D. | ∠A=∠ECD |
18.在实数范围内,$\sqrt{x+1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≥-1 | C. | x≤1 | D. | x≤-1 |
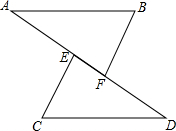 如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.
如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.