题目内容
4.计算(1)a•a5
(2)a•a5•a3
(3)(x4)3
(4)(y3)2•(y2)5
(5)(xy3n)2+(xy6)n
(6)(-3x3)2-[(2x)2]3
(7)(-xy)7÷(-xy)2=
(8)32m+1÷3m-1=
(9)(-3ab)(-a2c)2•6ab(c2)3
(10)(x+2)(x+3)
(11)(3x+2)(3x-2)
(12)20012-19992
(13)(2x-3)2
(14)($\frac{1}{3}$x+6y)2.
分析 (1)、(2)、(3)、(4)、(7)、(8)、(9)分别根据幂的运算法则进行计算即可;
(5)、(6)先根据幂的运算计算,再合并同类项即可;
(10)根据多项式乘以多项式计算即可;
(11)利用平方差公式计算;
(12)利用平方差公式分解因式即可;
(13)、(14)利用完全平方公式计算即可.
解答 解:
(1)a•a5=a6;
(2)a•a5•a3=a1+5+3=a9;
(3)(x4)3=x4×3=x12;
(4)(y3)2•(y2)5
=y6•y10
=y16;
(5)(xy3n)2+(xy6)n
=x2y6n+xny6n;
(6)(-3x3)2-[(2x)2]3
=9x6-(4x2)3
=9x6-64x6
=-55x6;
(7)(-xy)7÷(-xy)2
=(-xy)5
=-x5y5;
(8)32m+1÷3m-1=3(2m+1)-(m-1)=3m+2;
(9)(-3ab)(-a2c)2•6ab(c2)3
=(-3ab)(a4c2)×6abc6
=-18a6b2c8;
(10)(x+2)(x+3)
=x2+5x+6;
(11)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(12)20012-19992
=(2001+1999)×(2001-1999)
=4000×2
=8000;
(13)(2x-3)2
=(2x)2-2×2x×3+32
=4x2-12x+9;
(14)($\frac{1}{3}$x+6y)2
=($\frac{1}{3}$x)2+2×$\frac{1}{3}$x×6y+(6y)2
=$\frac{1}{9}$x2+4xy+36y2.
点评 本题主要考查乘法公式及同底数幂的运算,熟练掌握平方差公式、完全平方公式及同底数幂的运算法则是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若一元二次方程x2-2x-a=0没有实数根,则一次函数y=(a+1)x+(a-1)的图象不过第( )
| A. | 一象限 | B. | 二象限 | C. | 三象限 | D. | 四象限 |
9.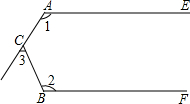 如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )
如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )
 如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )
如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
16.下列运算正确的是( )
| A. | -1-1=0 | B. | (2a2)3=6a6 | C. | a6÷a2=a3 | D. | (a+b)(a-b)=a2-b2 |
13.计算$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{48}$的结果是( )
| A. | 1 | B. | -1 | C. | -$\sqrt{3}$-$\sqrt{2}$ | D. | $\sqrt{2}$-$\sqrt{3}$ |
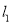 ,
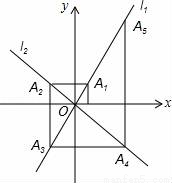
, 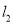 ,过点(1,0)作x轴的垂线交
,过点(1,0)作x轴的垂线交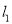 于点A1,过点A1作y轴的垂线交
于点A1,过点A1作y轴的垂线交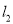 于点A2,过点A2作x轴的垂线交
于点A2,过点A2作x轴的垂线交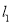 于点A3,过点A3作y轴的垂线交
于点A3,过点A3作y轴的垂线交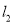 于点A4,…依次进行下去,则点A2015的坐标为__.
于点A4,…依次进行下去,则点A2015的坐标为__.