题目内容
8.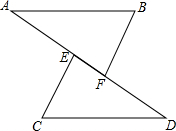 如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.
如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.(1)△ABF与△DCE全等吗?请说明理由;
(2)AB与CD平行吗?请说明理由.
分析 (1)先根据平行线的性质∠AFB=∠DEC,然后利用“ASA”可判断△ABF≌Rt△DCE;
(2)根据△ABF≌Rt△DCE,则∠A=∠D,再利用平行线的判定定理即可得到结论.
解答 证明:(1))△ABF与△DCE全等,理由是:
∵CE∥BF,
∴∠AFB=∠DEC,
在△ABF和△DCE中,
$\left\{\begin{array}{l}{∠AFB=∠DEC}\\{BF=CE}\\{∠B=∠C}\end{array}\right.$,
∴△ABF≌△DCE(ASA);
(2)AB与CD平行,理由是:
∵△ABF≌△DCE,
∴∠A=∠D(全等三角形的对应角相等),
∴AB∥CD.
点评 本题考查了全等三角形的判定以及平行线的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”、“HL”;全等三角形的对应角相等.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | -1-1=0 | B. | (2a2)3=6a6 | C. | a6÷a2=a3 | D. | (a+b)(a-b)=a2-b2 |
3.计算(-3ab3)2,所得结果正确的是( )
| A. | -6a2b3 | B. | 6a2b6 | C. | 9a2b6 | D. | 9a2b9 |
13.计算$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{48}$的结果是( )
| A. | 1 | B. | -1 | C. | -$\sqrt{3}$-$\sqrt{2}$ | D. | $\sqrt{2}$-$\sqrt{3}$ |