题目内容
2. 如图,△ABC和△DCE都是等边三角形,点B、C、E在同一直线上,AC与BD相交于M,DC与AE相交于点N.
如图,△ABC和△DCE都是等边三角形,点B、C、E在同一直线上,AC与BD相交于M,DC与AE相交于点N.(1)求证:BD=AE;
(2)△CMN是什么三角形?为什么?
分析 (1)利用等边三角形的性质证明△BCD≌△ACE就可以得出结论;
(2)△CMN是等边三角形,由△BCD≌△ACE可知∠CBM=∠CAN,根据ASA可证明△BCM≌△ACN,得到CM=CN,又∠MCN=60°,可知△CMN是等边三角形.
解答 (1)证明:∵△ABC与△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°.
∵∠ACB+∠ACD++∠DCE=180°,
∴∠ACD=60°,∠ACB+∠ACD=∠ACD+∠DCE,
即∠BCD=∠ACE.
在△BCD和△ACE中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE,
∴AE=BD;
(2)△CMN是等边三角形;
证明:∵△BCD≌△ACE,
∴∠CBM=∠CAN.
在△BCM和△ACN中
$\left\{\begin{array}{l}{∠CBM=∠CAN}\\{BC=AC}\\{∠ACB=∠ACD}\end{array}\right.$,
∴△BCM≌△ACN,
∴CM=CN,
∵∠ACB=∠DCE=60°,
∴∠MCN=60°,
∴△CMN是等边三角形.
点评 本题考查了等边三角形的性质的运用及全等三角形的判定和性质的运用.线段相等问题常常运用全等解决.

练习册系列答案
相关题目
13. 如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )
如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )
 如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )
如图是二次函数y=ax2+bx+c的图象,点P(a+b,bc)是坐标平面内的点,则点P在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
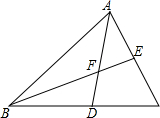 如图所示,△ABC的角平分线AD,BE相交于点F,∠C=60°,求证:AB=AE+BD.
如图所示,△ABC的角平分线AD,BE相交于点F,∠C=60°,求证:AB=AE+BD.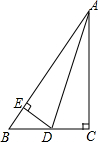 如图,AC⊥BD,AD平分∠BAC,DE⊥AB.试判断下面四个结论中哪些成立,哪些不成立.成立的,请说明理由;不成立的,请你在原有条件基础上再添加条件使之成立,并证明.(1)AD平分∠CDE;(2)∠BAC=∠BDE;(3)DE平分∠ADB;(4)BD+AC>AB.
如图,AC⊥BD,AD平分∠BAC,DE⊥AB.试判断下面四个结论中哪些成立,哪些不成立.成立的,请说明理由;不成立的,请你在原有条件基础上再添加条件使之成立,并证明.(1)AD平分∠CDE;(2)∠BAC=∠BDE;(3)DE平分∠ADB;(4)BD+AC>AB.