题目内容
11.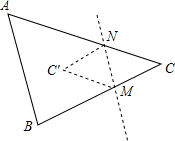 已知,如图,△ABC中,把点C沿直线MN对折得点C′.
已知,如图,△ABC中,把点C沿直线MN对折得点C′.(1)若∠C=30°,求∠ANC′+∠BMC′的度数,若∠C为40°呢?
(2)∠C与∠ANC′,∠BMC′有怎样的数量关系,并证明.
分析 (1)根据折叠的性质得到∠C′=∠C=30°,由四边形的内角和得到∠C′MC+∠C′NC=360°-∠C-∠C′=300°,于是得到结论;
(2)根据四边形的内角和得到∠C′MC+∠C′NC=360°-∠C-∠C′=300°,根据平角的定义即可得到结论.
解答 解:(1)∵把点C沿直线MN对折得点C′,
∴∠C′=∠C=30°,
∴∠C′MC+∠C′NC=360°-∠C-∠C′=300°,
∴∠ANC′+∠BMC′=180°-∠C′NC+180°-∠C′MC=360°-(∠C′MC+∠C′NC)=∠C+∠C′=2∠C=60°;
若∠C为40°时,
∠ANC′+∠BMC′=80°;
(2)∠ANC′+∠BMC′=2∠C,
∵∠C′MC+∠C′NC=360°-∠C-∠C′=300°,
∴∠ANC′+∠BMC′=180°-∠C′NC+180°-∠C′MC=360°-(∠C′MC+∠C′NC)=∠C+∠C′=2∠C.
点评 本题考查了翻折变换-折叠问题,四边形的内角和,平角的定义,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
16.将四个编号为1,2,3,4的小球随机放入4个编号为1,2,3,4的盒子中.记f(i)为第i个盒子中小球的编号与盒子编号的差的绝对值.则f(1)+f(2)+f(3)+f(4)=4的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{5}{24}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{24}$ |
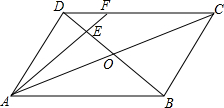 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.
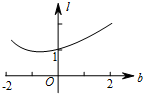
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.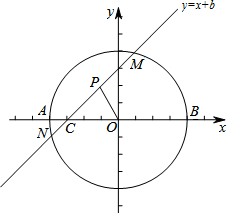 如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )
如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )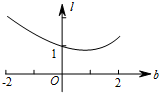


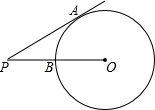 如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.
如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.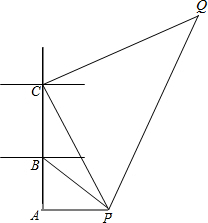 如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.
如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.