题目内容
6．先化简，再选择合适的x的值代入来计算分式的值：（x-1-$\frac{8}{x+1}$）÷$\frac{x+3}{x+1}$．分析 首先进行通分运算，进而因式分解法再化简分式，最后把符合题意的一个x的值代入求出答案．
解答 解：（x-1-$\frac{8}{x+1}$）÷$\frac{x+3}{x+1}$
=[$\frac{（x-1）（x+1）}{x+1}$-$\frac{8}{x+1}$]×$\frac{x+1}{x+3}$
=$\frac{（x+3）（x-3）}{x+1}$×$\frac{x+1}{x+3}$
=x-3，
当x=0时，原式=-3．
点评 此题主要考查了分式的化简求值，正确分解因式再化简分式是解题关键．
练习册系列答案
相关题目
一次函数y=ax+b的图象经过点A、点B，如图所示，则不等式0＜ax+b＜1的解集是-2＜x＜0．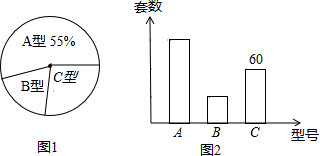
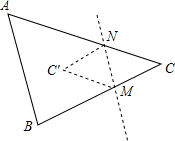已知，如图，△ABC中，把点C沿直线MN对折得点C′．