题目内容
16.将四个编号为1,2,3,4的小球随机放入4个编号为1,2,3,4的盒子中.记f(i)为第i个盒子中小球的编号与盒子编号的差的绝对值.则f(1)+f(2)+f(3)+f(4)=4的概率为( )| A. | $\frac{5}{16}$ | B. | $\frac{5}{24}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{24}$ |
分析 利用树状图法正确列举出所有结果,然后利用概率公式即可求解.
解答 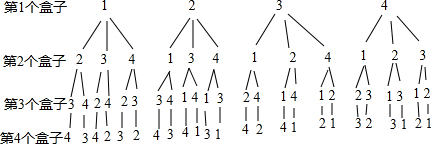
共有24种情况,满足f(1)+f(2)+f(3)+f(4)=4的有7种,
则概率为:$\frac{7}{24}$,
故选:D.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
8.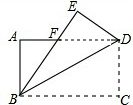 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{5}{13}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{7}$ |
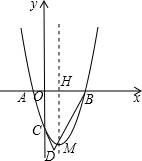 如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.
如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.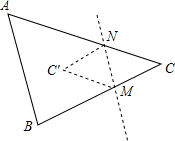 已知,如图,△ABC中,把点C沿直线MN对折得点C′.
已知,如图,△ABC中,把点C沿直线MN对折得点C′. 小明动手操作如下,先剪一个等腰三角形纸片ABC,使AB=AC,再把∠B沿EM折叠,使点B落在点D上;把∠C沿FN折叠,使点C落在点D上,则四边形AEDF是平行四边形,你认为正确吗?请说明理由.
小明动手操作如下,先剪一个等腰三角形纸片ABC,使AB=AC,再把∠B沿EM折叠,使点B落在点D上;把∠C沿FN折叠,使点C落在点D上,则四边形AEDF是平行四边形,你认为正确吗?请说明理由.