题目内容
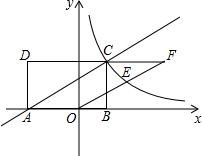 如图,矩形ABCD的顶点A、B的坐标分别为(-2,0)和(1,0),BC=2.反比例函数y=
如图,矩形ABCD的顶点A、B的坐标分别为(-2,0)和(1,0),BC=2.反比例函数y=| k |
| x |
(1)求k的值;
(2)若OE∥AC交反比例函数的图象于点E,交DC的延长线于点F.求:
①四边形AOFC的面积;
②点E的坐标.
考点:反比例函数综合题,平行四边形的判定与性质,相似三角形的性质
专题:综合题
分析:(1)求得点C的坐标,利用待定系数法即可求解;
(2)①证明四边形AOFC是平行四边形,利用平行四边形的面积公式即可求解;
②设E的坐标是(a,b),过点E作EH⊥x轴于H,可得△ABC∽△OHE,根据相似三角形的对应边的比相等,即可列方程求解.
(2)①证明四边形AOFC是平行四边形,利用平行四边形的面积公式即可求解;
②设E的坐标是(a,b),过点E作EH⊥x轴于H,可得△ABC∽△OHE,根据相似三角形的对应边的比相等,即可列方程求解.
解答:解:(1)∵B的坐标是(1,0),BC=2,
∴C的坐标是(1,2).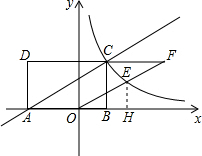
把C代入y=
得:k=2;
(2)①∵四边形ABCD是矩形,
∴CF∥AO,
又∵OE∥AC,
∴四边形AOFC是平行四边形.
∴四边形AOFC的面积为AO•CB=2×2=4;
②设E的坐标是(a,b),过点E作EH⊥x轴于H.
∵四边形ABCD是矩形,
∴CB⊥x轴,
∴∠ABC=∠OHE=90°,
又∵OE∥AC,
∴∠CAB=∠EOH,
∴△ABC∽△OHE,
∴
=
,即
=
,
又∵b=
.
解得:a=
,b=
.
则E的坐标是(
,
).
∴C的坐标是(1,2).

把C代入y=
| k |
| x |
得:k=2;
(2)①∵四边形ABCD是矩形,
∴CF∥AO,
又∵OE∥AC,
∴四边形AOFC是平行四边形.
∴四边形AOFC的面积为AO•CB=2×2=4;
②设E的坐标是(a,b),过点E作EH⊥x轴于H.
∵四边形ABCD是矩形,
∴CB⊥x轴,
∴∠ABC=∠OHE=90°,
又∵OE∥AC,
∴∠CAB=∠EOH,
∴△ABC∽△OHE,
∴
| AB |
| OH |
| CB |
| EH |
| 3 |
| a |
| 2 |
| b |
又∵b=
| 2 |
| a |
解得:a=
| 3 |
2
| ||
| 3 |
则E的坐标是(
| 3 |
2
| ||
| 3 |
点评:本题考查了待定系数法求函数的解析式,以及平行四边形的判定与性质,相似三角形的判定与性质,证明△ABC∽△OHE是关键.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目

 如图,正方形网格中的△ABC,若小方格边长为1.
如图,正方形网格中的△ABC,若小方格边长为1. 已知:如图,在△ABC中,BD平分∠ABC,且∠ADE=∠C.
已知:如图,在△ABC中,BD平分∠ABC,且∠ADE=∠C. 已知:如图,∠BAC与∠GCA互补,∠1=∠2,若∠E=46°,求∠F的度数.
已知:如图,∠BAC与∠GCA互补,∠1=∠2,若∠E=46°,求∠F的度数.