题目内容
如图，正方形网格中的△ABC，若小方格边长为1．（1）求△ABC的周长；
（2）△ABC是直角三角形吗？为什么？
考点：勾股定理,勾股定理的逆定理
专题：
分析：（1）根据勾股定理分别求出AB、BC、AC的长，再根据三角形周长的定义即可求解；
（2）根据勾股定理的逆定理判断出三角形ABC的形状．
（2）根据勾股定理的逆定理判断出三角形ABC的形状．
解答：解：（1）由勾股定理可得，AC=
=
；
BC=
=
；
AB=
=
=2
；
故△ABC的周长是
+3
；
（2）∵（
）2+（2
）2=（
）2，
∴AC2+AB2=BC2，
∴△ABC是直角三角形．
解：（1）由勾股定理可得，AC=| 32+22 |
| 13 |
BC=
| 82+12 |
| 65 |
AB=
| 62+42 |
| 52 |
| 13 |
故△ABC的周长是
| 65 |
| 13 |
（2）∵（
| 13 |
| 13 |
| 65 |
∴AC2+AB2=BC2，
∴△ABC是直角三角形．
点评：本题考查了勾股定理、勾股定理逆定理、三角形的周长，充分利用网格是解题的关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
已知
-
=3，则
的值是（ ）
| 1 |
| x |
| 2 |
| y |
| 2xy |
| 2x-y |
| A、-3 | ||
B、
| ||
C、-
| ||
| D、2 |
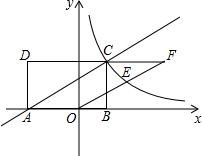如图，矩形ABCD的顶点A、B的坐标分别为（-2，0）和（1，0），BC=2．反比例函数y=
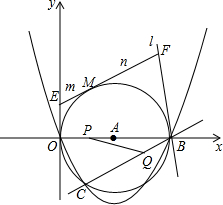如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+bx+c（a≠0）过O、B、C三点，B、C坐标分别为（10，0）和（
