题目内容
18.[问题提出]:如图1,由n×n×n(长×宽×高)个小立方块组成的正方体中,到底有多少个长方体(包括正方体)呢?
[问题探究]:我们先从较为简单的情形入手.
(1)如图2,由2×1×1个小立方块组成的长方体中,长共有1+2=$\frac{2×3}{2}$=3条线段,宽和高分别只有1条线段,所以图中共有3×1×1=3个长方体.
(2)如图3,由2×2×1个小立方块组成的长方体中,长和宽分别有1+2=$\frac{2×3}{2}$=3条线段,高有1条线段,所以图中共有3×3×1=9个长方体.
(3)如图4,由2×2×2个小立方体组成的正方体中,长、宽、高分别有1+2=$\frac{2×3}{2}$=3条线段,所以图中共有27个长方体.
(4)由2×3×6个小立方块组成的长方体中,长共有1+2=$\frac{3×2}{2}$=3条线段,宽共有6条线段,高共有21条线段,所以图中共有63个长方体.
[问题解决]
(5)由n×n×n个小立方块组成的正方体中,长、宽、高各有$\frac{n(n+1)}{2}$线段,所以图中共有$\frac{{n}^{3}(n+1)^{3}}{8}$个长方体.
[结论应用]
(6)如果由若干个小立方块组成的正方体中共有1000个长方体,那么组成这个正方体的小立方块的个数是多少?请通过计算说明你的结论.
分析 [问题探究]:
(3)如图4,把长、宽、高三边的线段条数相乘即可求解;
(4)先得到宽共有多少条线段,高共有多少条线段,再把长、宽、高三边的线段条数相乘即可求解;
(5)先根据数线段的方法得到长、宽、高三边的线段条数,再把它们相乘即可求解;
[结论应用]
(6)由(5)的结论,根据等量关系:由若干个小立方块组成的正方体中共有1000个长方体,列出方程求解即可.
解答 解:[问题探究]:
(3)3×3×3=27(个).
答:图中共有27个长方体.
(4)4×3÷2=6(条),
7×6÷2=21(条),
3×6×21=378(个).
答:宽共有6条线段,高共有21条线段,图中共有63个长方体.
(5)长、宽、高各有$\frac{n(n+1)}{2}$线段,所以图中共有[$\frac{n(n+1)}{2}$]3=$\frac{{n}^{3}(n+1)^{3}}{8}$个长方体.
[结论应用]
(6)依题意有:
[$\frac{n(n+1)}{2}$]3=1000,
$\frac{n(n+1)}{2}$=10,
解得n1=4,n2=-5(不合题意舍去),
4×4×4=64(个).
答:组成这个正方体的小立方块的个数是64个.
故答案为:27;6,21,63;$\frac{n(n+1)}{2}$,$\frac{{n}^{3}(n+1)^{3}}{8}$.
点评 考查了立体图形,组合图形中线段的计数,本题关键是得到n×n×n个小立方块组成的正方体中共有[$\frac{n(n+1)}{2}$]3个长方体.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若$\root{3}{0.3670}$=0.7160,$\root{3}{3.670}$=1.542,则$\root{3}{367}$=7.16,$\root{3}{-3670}$=-15.42.
6.出租车司机小王某天下午营运全是在东西走向的汶河大道上进行的,如果规定向东为正,向西为负,这天下午他的行车里程(单位:千米)如下表所示:
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.1升/千米,这天下午小王共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | 第十一次 |
| +15 | -2 | +5 | -1 | +10 | -3 | -2 | +12 | +4 | -5 | +6 |
(2)若汽车耗油量为0.1升/千米,这天下午小王共耗油多少升?
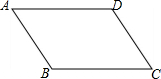 如图,已知四边形ABCD是平行四边形,AB<AD.
如图,已知四边形ABCD是平行四边形,AB<AD.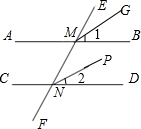 如图,直线AB和直线CD被直线EF所截,∠BMN=∠DNF,∠1=∠2,那么MG与NP平行吗?请说明理由.
如图,直线AB和直线CD被直线EF所截,∠BMN=∠DNF,∠1=∠2,那么MG与NP平行吗?请说明理由.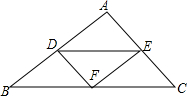 如图,△ABC是由四个形状、大小完全一样的三角形拼成,则可以看着是由△ADE平移得到的小三角形是△DBF或△EFC.
如图,△ABC是由四个形状、大小完全一样的三角形拼成,则可以看着是由△ADE平移得到的小三角形是△DBF或△EFC.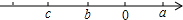 已知实数a,b,c在数轴上的位置如图所示,试化简$\sqrt{{{({a+c})}^2}}-\left|{b-c}\right|$.
已知实数a,b,c在数轴上的位置如图所示,试化简$\sqrt{{{({a+c})}^2}}-\left|{b-c}\right|$.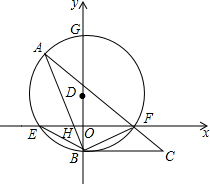 如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.
如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.