题目内容
7.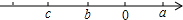 已知实数a,b,c在数轴上的位置如图所示,试化简$\sqrt{{{({a+c})}^2}}-\left|{b-c}\right|$.
已知实数a,b,c在数轴上的位置如图所示,试化简$\sqrt{{{({a+c})}^2}}-\left|{b-c}\right|$.
分析 根据数轴得出c<b<0<a,|c|>|a|,|c|>|b|,先根据二次根式性质进行计算,再去掉绝对值符号,最后合并即可.
解答 解:∵从数轴可知:c<b<0<a,|c|>|a|,|c|>|b|,
∴$\sqrt{(a+c)^{2}}$-|b-c|
=|a+c|-|b-c|
=-(a+c)-(b-c)
=-a-c-b+c
=-a-b.
点评 本题考查了二次根式的性质,绝对值,数轴的应用,能正确根据二次根式的性质和绝对值法则进行计算是解此题的关键.

练习册系列答案
相关题目
19. 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )
 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )| A. | AC⊥BD | B. | AC=BD | C. | AB=AD | D. | AO=CO |
16.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x-5y=8}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x=y+z}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |

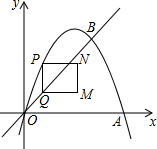 如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).
如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).