Question

8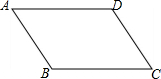．如图，已知四边形ABCD是平行四边形，AB＜AD．
（1）利用尺规作∠BAD的平分线AG，交BC于点E，记点B关于AE对称的点为F（求保留作图痕迹，不写作法）；
（2）在（1）所作的图中，若BF=6，AB=5，求AE的长．

Answer 1

分析 （1）根据要求画出图形即可．
（2）在RT△AOB中求出AO，证明AE=2AO即可．

解答 解：（1）①∠BAD的平分线AG，交BC于点E，②作BF⊥AE交AD于F，则点B、F关于AE对称，图象如图所示，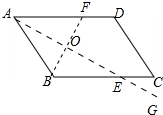

（2）设AE与BF交于点O，
∵AE垂直平分BF，
∴BO=$\frac{1}{2}$FB=3，
在RT△AOB中，∵∠AOB=90°，AB=5，BO=3，
∴AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠FAO=∠AEB=∠BAE，
∴BA=BE，
∵BF⊥AE，
∴AO=OE=4，
∴AE=8．

点评 本题考查平行四边形的性质、角平分线、对称、等腰三角形的性质、勾股定理等知识，解题的关键是证明△ABE是等腰三角形，利用等腰三角形的性质解决问题，属于中考常考题型．