题目内容
11.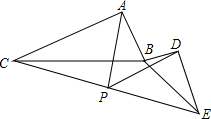 如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.
如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.
分析 根据已知条件AC=k•AB,DE=k•DB,得到△ABC∽△BDE,求出∠ABC=∠DBE,分别取BC,BE的中点M,N,连接AM,PM,DN,PN,根据三角形的中位线定理得到AM=PN=$\frac{1}{2}$BC,DN=PM=$\frac{1}{2}$BE,PM∥BN,PN∥BM,于是得到四边形PNBM是平行四边形,得到∠BMP=∠BNP,证得△AMP≌△PND,即可得到结论AP=DP.
解答  解:PA=PD,
解:PA=PD,
∵AC=k•AB,DE=k•DB,
∴$\frac{AC}{AB}=\frac{DE}{BD}=k$,
∵∠CAB=∠BDE=90°,
∴△ABC∽△BDE,
∴∠ABC=∠DBE,
分别取BC,BE的中点M,N,
连接AM,PM,DN,PN,
∵P为CE中点,
∴AM=PN=$\frac{1}{2}$BC,DN=PM=$\frac{1}{2}$BE,
∴PM∥BN,PN∥BM,
∴四边形PNBM是平行四边形,
∴∠BMP=∠BNP,
∵AM=BM.DN=BN,
∴∠ABM=∠MAB=∠NBD=∠NDB,
∴∠AMB=∠BND,
∴∠AMB+∠BMP=∠DNB+∠BNP,
即∠AMP=∠DNP,
在△AMP与△PND中,$\left\{\begin{array}{l}{AM=PN}\\{∠AMP=∠PND}\\{PM=DN}\end{array}\right.$,
∴△AMP≌△PND,
∴AP=DP.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定与性质,直角三角形的性质,三角形的中位线定理,正确的周长辅助线构造全等三角形是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
2.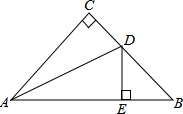 如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
 如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )
如图,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB周长为( )| A. | 4cm | B. | 6cm | C. | 10cm | D. | 14cm |
16.北京国家体育场面积达25.6万平方米,用科学记数法表示应为( )
| A. | 25.6×104㎡ | B. | 25.6×105㎡ | C. | 2.56×105㎡ | D. | 2.56×106㎡ |
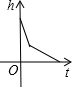
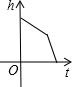
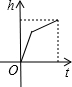
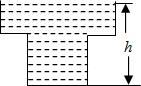 某蓄水池的横截面示意图如图所示,分深水区和浅水区.如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间关系的是( )
某蓄水池的横截面示意图如图所示,分深水区和浅水区.如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间关系的是( )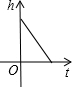
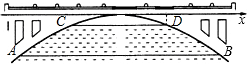 如图是一抛物线状拱桥,正常水位时,桥下的水面宽AB为20m,当水面上升3m到达警戒水位时,水面宽CD为10m
如图是一抛物线状拱桥,正常水位时,桥下的水面宽AB为20m,当水面上升3m到达警戒水位时,水面宽CD为10m