题目内容
6.已知抛物线y=-(x-2)2+m2(常数>0)的顶点为P.设此抛物线与x轴的两个交点从左至右依次为点A,B.又知∠APB=120°,则△APB的周长是$\frac{2\sqrt{3}+4}{3}$.分析 求△ABP的周长,关键是确定三角形三顶点的坐标.可先根据抛物线的解析式用m表示出A、B两点的横坐标,那么AB的差就是这两个横坐标的差的绝对值,由于∠APB=90°,可得出△APB是等腰直角三角形,因此P点的纵坐标的绝对值应该是AB长的一半,由此可求出m的值,进而可求出A、B、P三点的坐标,即可求出△ABP的周长.
解答 解:设A、B两点坐标分别为A(x1,0)、B(x2,0).
由-(x-2)2+m2=0,
∵m>0,
∴x1=-m+2,x2=m+2.
AB=x2-x1=(m+2)-(-m+2)=2m.
∵P为抛物线的顶点.
又∵抛物线对称轴为AB的垂直平分线,设对称轴于AB交于点D,
∴∠PAB=30°.
∴AD=$\sqrt{3}$PD
∴2$\sqrt{3}$PD=AB.
即2$\sqrt{3}$m2=2m.
∵m>0.
∴m=$\frac{\sqrt{3}}{3}$
由此可求得:AB=$\frac{2\sqrt{3}}{3}$,AP=BP=$\frac{2}{3}$,
∴△APB的周长为$\frac{2\sqrt{3}+4}{3}$.
故答案为:$\frac{2\sqrt{3}+4}{3}$.
点评 本题考查了二次函数的性质以及一元二次方程根与系数的关系(即韦达定理).

练习册系列答案
相关题目
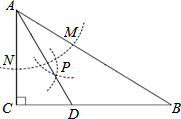 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;正确的个数是3 个.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;正确的个数是3 个.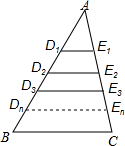 如图,△ABC中,BC=a.
如图,△ABC中,BC=a.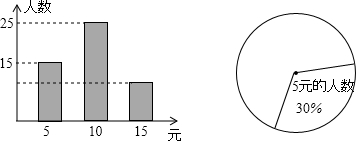
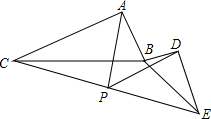 如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.
如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.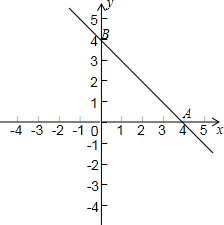 右图是直线y=-x+4在平面直角坐标系中的函数图象,与x轴和y轴的交点分别为点A(4,0)和点B(0,4).
右图是直线y=-x+4在平面直角坐标系中的函数图象,与x轴和y轴的交点分别为点A(4,0)和点B(0,4). 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=2,AF=3,?ABCD的周长为25,则?ABCD的面积为15.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=2,AF=3,?ABCD的周长为25,则?ABCD的面积为15.