题目内容
1.若a=$\frac{1}{2-\sqrt{5}}$,b=$\frac{1}{2+\sqrt{5}}$,则a+b+ab的值-5.分析 首先把a、b分母有理化,再代入计算即可.
解答 解:∵a=$\frac{1}{2-\sqrt{5}}$=$\frac{2+\sqrt{5}}{(2-\sqrt{5})(2+\sqrt{5})}$=-2-$\sqrt{5}$,
b=$\frac{1}{2+\sqrt{5}}$=$\frac{2-\sqrt{5}}{(2+\sqrt{5})(2-\sqrt{5})}$=-2+$\sqrt{5}$,
∴a+b+ab
=-2-$\sqrt{5}$-2+$\sqrt{5}$+(-2-$\sqrt{5}$)(-2+$\sqrt{5}$)
=-4+(-2)2-($\sqrt{5}$)2
=-4+4-5
=-5.
故答案为:-5.
点评 本题考查了二次根式的化简求值、分母有理化、平方差公式;熟练掌握分母有理化是解决问题的关键.

练习册系列答案
相关题目
11.已知m是方程x2-x-2=0的一个根,则代数式m2-m的值为( )
| A. | 4 | B. | 2 | C. | 8 | D. | -2 |
12.武汉东湖高新开发区某企业新增了一个项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.设购买A种型号的污水处理设备x台,可列不等式组$\left\{\begin{array}{l}{12x+10(8-x)≤89}\\{200x+160(8-x)≥1380}\end{array}\right.$.
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 月污水处理能力(吨/月) | 200 | 160 |
6.今年我市有近2万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这1000名考生是总体的一个样本 | B. | 近2万名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 1000名学生是样本容量 |
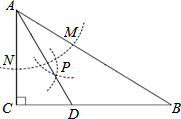 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;正确的个数是3 个.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;正确的个数是3 个.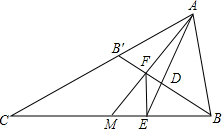 如图,已知在△ABC中,M是BC的中点,AE是∠BAC的平分线,过B作BD⊥AE,垂足为D,AM与BD相交于F,求证:EF∥AB.
如图,已知在△ABC中,M是BC的中点,AE是∠BAC的平分线,过B作BD⊥AE,垂足为D,AM与BD相交于F,求证:EF∥AB.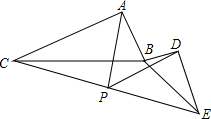 如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.
如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.