题目内容
1.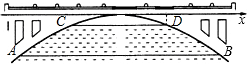 如图是一抛物线状拱桥,正常水位时,桥下的水面宽AB为20m,当水面上升3m到达警戒水位时,水面宽CD为10m
如图是一抛物线状拱桥,正常水位时,桥下的水面宽AB为20m,当水面上升3m到达警戒水位时,水面宽CD为10m(1)请你在图中建立恰当的平面直角坐标系,并求出拱桥的抛物线解析式;
(2)当水位到达警戒水位时,继续以0.2m/s的速度上涨,那么再过多长时间此桥孔将被淹没.
分析 (1)以拱桥最顶端为原点,建立直角坐标系,设抛物线解析式为y=ax2,因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,设点B(10,n),点D(5,n+3),代入数据可求出函数解析式.
(2)首先计算出D点纵坐标,再求时间即可.
解答  解:(1)设抛物线解析式为y=ax2,
解:(1)设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,
所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
由题意:$\left\{\begin{array}{l}{n=100a}\\{n+3=25a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{n=-4}\\{a=-\frac{1}{25}}\end{array}\right.$,
∴y=-$\frac{1}{25}$x2.
(2)∵n=-4,
∴D点纵坐标为-4+3=-1,
1÷0.2=5(小时).
答:再过5小时时间此桥孔将被淹没.
点评 此题主要考查了二次函数的应用,关键是正确建立坐标系,表示出B、D点坐标求出解析式.

练习册系列答案
相关题目
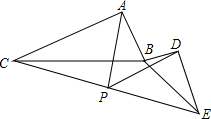 如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.
如图,△ABC与△BDE中,∠CAB=∠BDE=90°,AC=k•AB,DE=k•DB,P为CE中点,连接PA,PD,探究PA,PD的数量关系.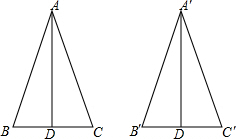 如图,AD、A′D′分别是BC和B′C′上的高,且∠B=∠B′,$\frac{A′D′}{AD}$=$\frac{B′C′}{BC}$,求证:△ABC∽△A′B′C.
如图,AD、A′D′分别是BC和B′C′上的高,且∠B=∠B′,$\frac{A′D′}{AD}$=$\frac{B′C′}{BC}$,求证:△ABC∽△A′B′C.
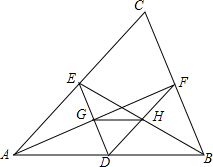 如图所示,D为△ABC的边AB上的点,过D点作DE∥BC、DF∥AC,AF交DE于点G,BE交DF于点H,求证:GH∥AB.
如图所示,D为△ABC的边AB上的点,过D点作DE∥BC、DF∥AC,AF交DE于点G,BE交DF于点H,求证:GH∥AB.