题目内容
2.在五水共治工作中,有一段长为540米的河道整治任务由A、B两个工程队先后接力完成,A工程队每天整治河道18米,B工程队每天整治河道12米.(1)若完成河道整治任务共用了40天.
①根据题意,甲、乙两个同学分别通过列方程组来解决:

则甲列出的方程组为$\left\{\begin{array}{l}{x+y=40}\\{18x+12y=540}\end{array}\right.$;乙列出的方程组中,a表示A工程队整治河道的米数,b表示B工程队整治河道的米数;
②求A、B两工程队分别整治河道多少米?(写出完整的解答过程).
分析 ①此题蕴含两个基本数量关系:A工程队用的时间+B工程队用的时间=20天,A工程队整治河道的米数+B工程队整治河道的米数=180,由此进行解答即可;根据乙所列方程组得到a和b表示的含义;
②根据乙的方程组解答解决问题.
解答 解:①根据题意,甲:x表示A工程队用的时间,y表示B工程队用的时间;
乙:x表示A工程队整治河道的米数,y表示B工程队整治河道的米数;
设A工程队用的时间为x天,B工程队用的时间为y天,由此列出的方程组为:
$\left\{\begin{array}{l}{x+y=40}\\{18x+12y=540}\end{array}\right.$,
A工程队整治河道的米数为a,B工程队整治河道的米数为b,由此列出的方程组为:
$\left\{\begin{array}{l}{a+b=540}\\{\frac{a}{18}+\frac{b}{12}=40}\end{array}\right.$.
②乙:$\left\{\begin{array}{l}{a+b=540}\\{\frac{a}{18}+\frac{b}{12}=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=180}\\{b=360}\end{array}\right.$.
答:A、B两工程队分别整治河道180m,360m.
故答案为:$\left\{\begin{array}{l}{x+y=40}\\{18x+12y=540}\end{array}\right.$;A工程队整治河道的米数,B工程队整治河道的米数.
点评 此题主要考查了二元一次方程组的应用,利用基本数量关系:A工程队用的时间+B工程队用的时间为40天,A工程队整治河道的米数+B工程队整治河道的米数=540,运用不同设法列出不同的方程组解决实际问题.

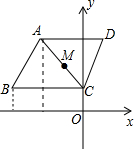 如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )
如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )| A. | (-2017,2) | B. | (-2017,-2) | C. | (-2018,-2) | D. | (-2018,2) |
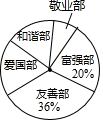 小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示.
小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示. | 福卡 | 和谐福 | 富强福 | 爱国福 | 友善福 | 敬业福 |
| 人数 | 21 | 20 | a | b | 8 |
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“爱国福”部分所对应的扇形的圆心角度数;
(3)若只在这些友好之间转赠福卡,则这次最多有多少人可收集到“五福”?
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 1 | D. | 2 |
| A. |  直角三角形 | B. |  正五边形 | C. |  正方形 | D. |  平行四边形 |
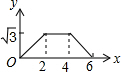
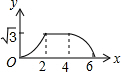
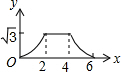
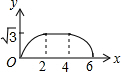
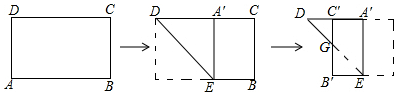
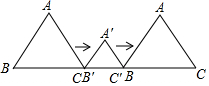 如图,边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示,它们的边BC、B′C′位于同一条直线l上,点C与B′重合,△A′B′C′固定不动,然后把△ABC自左向右沿直线l平移,移出△A′B′C′外(点B与C′重合)停止,设△ABC平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
如图,边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示,它们的边BC、B′C′位于同一条直线l上,点C与B′重合,△A′B′C′固定不动,然后把△ABC自左向右沿直线l平移,移出△A′B′C′外(点B与C′重合)停止,设△ABC平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )