题目内容
12．
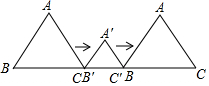如图，边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示，它们的边BC、B′C′位于同一条直线l上，点C与B′重合，△A′B′C′固定不动，然后把△ABC自左向右沿直线l平移，移出△A′B′C′外（点B与C′重合）停止，设△ABC平移的距离为x，两个三角形重合部分的面积为y，则y关于x的函数图象是（ ）| A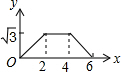． |  | B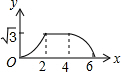． |  | C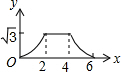． |  | D． |  |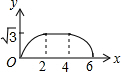
分析 当0≤x＜2时，B′C=x，y=$\frac{\sqrt{3}}{4}$B′C2=$\frac{\sqrt{3}}{4}$x2；当2≤x≤4时，重合部分的面积就是△A′B′C′的面积，y=$\frac{\sqrt{3}}{4}$B′C′2=$\sqrt{3}$；当4＜x≤6时，BC′=6-x，y=$\frac{\sqrt{3}}{4}$（6-x）2，由此即可判定．
解答 解：当0≤x＜2时，B′C=x，y=$\frac{\sqrt{3}}{4}$B′C2=$\frac{\sqrt{3}}{4}$x2；
当2≤x≤4时，重合部分的面积就是△A′B′C′的面积，y=$\frac{\sqrt{3}}{4}$B′C′2=$\sqrt{3}$；
当4＜x≤6时，BC′=6-x，y=$\frac{\sqrt{3}}{4}$（6-x）2，
结合选项可知选C．
故选C．
点评 本题主要考查了动点问题的函数图象，解题的关键是学会构建分段函数解决问题，属于中考常考题型．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形，建立如图所示的平面直角坐标系，点C的坐标为（0，-1）．
7．
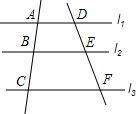如图，若l1∥l2∥l3，则下列各式错误的是（ ）
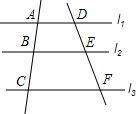如图，若l1∥l2∥l3，则下列各式错误的是（ ）| A． | $\frac{BC}{AC}$=$\frac{EF}{DF}$ | B． | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | C． | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | D． | $\frac{AB}{AC}$=$\frac{DE}{EF}$ |
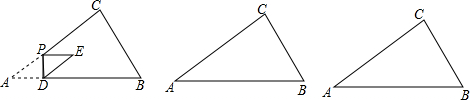
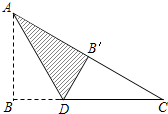如图，Rt△ABC中，∠B=90°，AB=3，BC=4，将△ABC折叠，使点B恰好落在斜边AC上，与点B′重合，AD为折痕，求DB′的长．
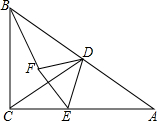如图，在Rt△ABC中，∠C=90°，∠A=30°．点D是AB中点，点E为边AC上一点，连接CD，DE，以DE为边在DE的左侧作等边三角形DEF，连接BF．