题目内容
14．小华和小军做摸球游戏：A袋装有编号为1，2，3的三个小球，B袋装有编号为4，5，6的三个小球，两袋中的所有小球除编号外都相同．从两个袋子中分别随机摸出一个小球，若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数，则小华胜，否则小军胜．这个游戏对双方公平吗？请说明理由．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与数字的差为偶数的情况，再利用概率公式求解即可求得答案．
解答 解：不公平，
画树状图得：
∵共有9种等可能的结果，数字的差为偶数的有4种情况，
∴P（小华胜）=$\frac{4}{9}$，P（小军胜）=$\frac{5}{9}$，
∵$\frac{4}{9}$≠$\frac{5}{9}$，
∴这个游戏对双方不公平．
点评 本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
5．
如图所示，反比例函数y=$\frac{1}{x}$与直线y=-x+2只有一个公共点P，则称P为切点．若反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M，则当k＜0时切点M的坐标是（ ）
如图所示，反比例函数y=$\frac{1}{x}$与直线y=-x+2只有一个公共点P，则称P为切点．若反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M，则当k＜0时切点M的坐标是（ ）| A． | （-1，3） | B． | （3，-1） | C． | （1，3） | D． | （-3，1） |
19．
一个几何体由n个大小相同的小正方体搭成，其左视图、俯视图如图所示，则n的最小值是（ ）
一个几何体由n个大小相同的小正方体搭成，其左视图、俯视图如图所示，则n的最小值是（ ）| A． | 5 | B． | 7 | C． | 9 | D． | 10 |
6．
甲、乙、丙、丁四名射击运动员在选拔赛中，每人射击了10次，甲、乙两人的成绩如表所示．丙、丁两人的成绩如图所示．欲选一名运动员参赛，从平均数与方差两个因素分析，应选（ ）
甲、乙、丙、丁四名射击运动员在选拔赛中，每人射击了10次，甲、乙两人的成绩如表所示．丙、丁两人的成绩如图所示．欲选一名运动员参赛，从平均数与方差两个因素分析，应选（ ）| 甲 | 乙 | |
| 平均数 | 9 | 8 |
| 方差 | 1 | 1 |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
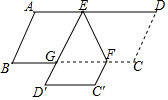如图，E，F分别是?ABCD的边AD、BC上的点，EF=6，∠DEF=60°，将四边形EFCD沿EF翻折，得到EFC′D′，ED′交BC于点G，则△GEF的周长为（ ）