题目内容
6.深化理解:新定义:对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果n-$\frac{1}{2}$≤x<n+$\frac{1}{2}$,则<x>=n;
反之,当n为非负整数时,如果<x>=n,则n-$\frac{1}{2}$≤x<n+$\frac{1}{2}$.
例如:<0>=<0.48>=0,<0.64>=<1.49>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
填空:①<π>=3(π为圆周率);
②如果<x-1>=3,则实数x的取值范围为3.5≤x<4.5.
若关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-4}{3}≤x-1}\\{<a>-x>0}\end{array}\right.$的整数解恰有3个,求a的取值范围.
①关于x的分式方程$\frac{1-<m>x}{x-2}$+2=$\frac{1}{2-x}$有正整数解,求m的取值范围;
②求满足<x>=$\frac{4}{3}$x 的所有非负实数x的值.
分析 ①利用对非负实数x“四舍五入”到个位的值记为<x>,进而得出<π>的值;
②利用对非负实数x“四舍五入”到个位的值记为<x>,进而得出x的取值范围;
首先将<a>看作一个字母,解不等式组进而根据整数解的个数得出a的取值范围;
①先解方程,得出x=$\frac{2}{2-<m>}$,再根据2-<m>是整数,x是正整数,得到2-<m>=1或2,进而得出<m>=0,则0≤m<0.5;
②利用<x>=$\frac{4}{3}$x,设$\frac{4}{3}$x=k,k为整数,得出关于k的不等关系求出即可.
解答 解:①由题意可得:<π>=3;
故答案为:3,
②∵<x-1>=3,
∴2.5≤x-1<3.5,
∴3.5≤x<4.5;
故答案为:3.5≤x<4.5;
解不等式组得:-1≤x<<a>,
由不等式组整数解恰有3个得,1<<a>≤2,
故1.5≤a<2.5;
①解方程得x=$\frac{2}{2-<m>}$,
∵2-<m>是整数,x是正整数,
∴2-<m>=1或2,
2-<m>=1时,x=2是增根,舍去.
∴2-<m>=2,
∴<m>=0,
∴0≤m<0.5.
②∵x≥0,$\frac{4}{3}$x为整数,设$\frac{4}{3}$x=k,k为整数,
则x=$\frac{3}{4}$k,
∴<$\frac{3}{4}$k>=k,
∴k-$\frac{1}{2}$≤$\frac{3}{4}$k<k+$\frac{1}{2}$,k≥0,
∴0≤k≤2,
∴k=0,1,2,
则x=0,$\frac{3}{4}$,$\frac{3}{2}$.
点评 此题主要考查了一元一次不等式组的应用,新定义以及分式方程的解,根据题意正确理解<x>的意义是解题关键.

练习册系列答案
相关题目
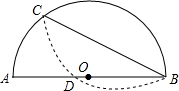 以半圆的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若tanB=$\frac{1}{2}$,且AD=4,则AB=10.
以半圆的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若tanB=$\frac{1}{2}$,且AD=4,则AB=10.
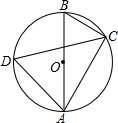 如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°.