题目内容
1.如图3,在等腰△ABC中,AB=AC,D是BC边上任一点,连接AD,过点B作BE∥AC,且AD=DE,连接DE.(1)求证:∠E=∠BAD;
(2)当D为BC中点时,作DF⊥AC于点F,作AH⊥BF分别交BF、DF于点H、G,求证:G为DF的中点;
(3)设DE交AB于点M,若$\frac{AM}{BM}=\frac{8}{3}$,在(2)的条件下,请直接写出:cos∠C的值为$\frac{\sqrt{5}}{5}$.
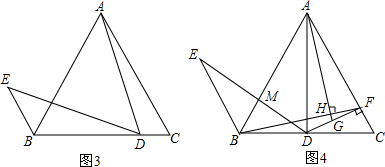
分析 (1)如图3中,DP⊥EB,DQ⊥AB垂足分别为P、Q,只要证明△ADQ≌△EDP即可.
(2)如图4中取BF中点M,连接DM、MG、DH,只要证明MG∥BD即可.
(3)如图5中,作BH⊥AC于H,DR⊥AE于R,交AB于K,由A、E、B、D四点共圆得∠AEB=90°,先证明四边形AEBH是矩形,设AK=BK=KD=11k,由KD∥BE得$\frac{KM}{BM}=\frac{KD}{EB}=\frac{5}{6}$,用k表示出EB、AH、BH、CH、BC,在RT△BCH中可以求出cos∠C.
解答 (1)证明:如图3中,作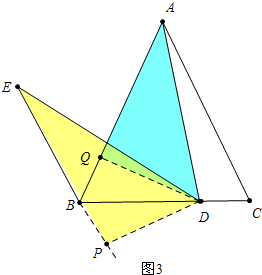 DP⊥EB,DQ⊥AB垂足分别为P、Q,
DP⊥EB,DQ⊥AB垂足分别为P、Q,
∵BE∥AC,
∴∠C=∠PBC,
∵AB=AC,
∴∠ABC=∠C,
∴∠ABC=∠PBC,
∵DP⊥EB,DQ⊥AB,
∴PD=DQ,∠AQD=∠EPD=90°,
在RT△ADQ和RT△EDP中,
$\left\{\begin{array}{l}{AD=ED}\\{DQ=DP}\end{array}\right.$,
∴△ADQ≌△EDP,
∴∠E=∠BAD.
(2)如图4中取BF中点M,连接DM、MG、DH、AE.
∵BD=DC,BM=MF,
∴DM∥AC,
∵DF⊥AC,AG⊥BF
∴∠MDF=∠DFC=90°=∠MHG,
∴∠MDG+∠MHG=180°,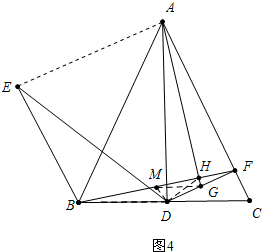
∴D、M、H、G四点共圆,
∴∠DGM=∠MHD,
∵∠BDA=∠AHM=90,
∴A、B、D、H四点共圆,
∴∠BAD=∠MHD=∠MGD,
∵AB=AC,BD=DC,
∴∠BAD=∠DAC,
∵∠DAC+∠C=90°,∠CDF+∠C=90°,
∴∠DAC=∠CDF
∴∠CDF=∠MGD,
∴MG∥BD,
∵FM=MB,
∴FG=DG即点G是DF中点.
(3)如图5中,作BH⊥AC于H,DR⊥AE于R,交AB于K.
∵∠BED=∠BAD,
∴A、E、B、D四点共圆,
∴∠AEB+∠ADB=180°,∵∠ADB=90°,
∴∠AEB=90°,
∵BE∥AC,
∴∠AEB+∠EAC=180°,
∴∠EAC=90°,
∵∠AEB=∠EAH=∠AHB=90°,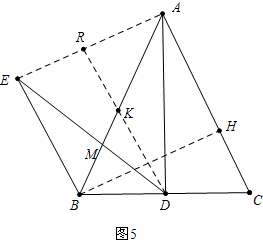
∴四边形AEBH是矩形,
∴BE=AH,
∵∠ERD=∠EAC=90°,
∴DR∥AC,
∵BD=DC,
∴AK=BK=KD,设AK=BK=KD=11k,
∵AM:BM=8:3,
∴AM=16k,BM=6k,MK=5k,
∵KD∥BE,
∴$\frac{KM}{BM}=\frac{KD}{EB}=\frac{5}{6}$,
∴$EB=\frac{66}{5}k$=AH,
∴BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\frac{88}{5}k$,CH=CA-AH=$\frac{44}{5}k$,
∴BC=$\sqrt{B{H}^{2}+C{H}^{2}}$=$\frac{44\sqrt{5}}{5}k$,
∴cos∠C=$\frac{CH}{BC}$=$\frac{\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$.
点评 本题考查全等三角形的判定和性质、四点共圆的判定和性质、矩形的判定和性质,综合性比较强,添加辅助线构造全等三角形是解决问题的关键,学会用方程的思想去思考问题,属于中考压轴题.

| A. | AD=CD | B. | ∠B+∠D=180° | C. | AC=2AB | D. | 对角线互相垂直 |
 如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE
如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE