题目内容
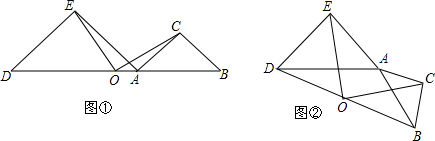
11.如图,△ABC与△ADE都是等腰直角三角形,∠ACB=∠AED=90°,连接DB,O为DB的中点,连接OE,OC.(1)如图①,当A,B,D三点共线时,求证:OC=OE且OC⊥OE;
(2)如图②,当A,B,D三点不共线时,(1)的结论是否成立?说明理由.
分析 (1)如图1,延长EO到F使OF=OE,连接EC,BF,CF,通过△DOE≌△BOF,得到DE=BF,∠D=∠OBF,证得△ACE≌△BCF,根据全等三角形的性质得到EC=CF,∠ACE=∠BCF,推出△ECF是等腰直角三角形,根据等腰直角三角形的性质即可得到结论;
(2)延长EO到F使OF=OE,连接EC,BF,CF,通过△DOE≌△BOF,得到DE=BF,∠D=∠OBF,证得△ACE≌△BCF,根据全等三角形的性质得到EC=CF,∠ACE=∠BCF,推出△ECF是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.
解答 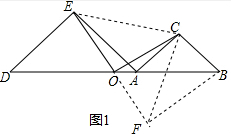 解:(1)如图1,延长EO到F使OF=OE,连接EC,BF,CF,
解:(1)如图1,延长EO到F使OF=OE,连接EC,BF,CF,
在△DOE与△BOF中,$\left\{\begin{array}{l}{DO=BO}\\{∠DOE=∠BOF}\\{EO=FO}\end{array}\right.$,
∴△DOE≌△BOF,
∴DE=BF,∠D=∠OBF,
∴AE=BF,
∵△ABC与△ADE都是等腰直角三角形,∠ACB=∠AED=90°,
∴∠D=∠ABC=∠EAD=∠CAB=45°,
∴∠CAE=∠CBF=90°,
在△ACE与△BCF中,$\left\{\begin{array}{l}{AE=BF}\\{∠EAC=∠FBC}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCF,
∴EC=CF,∠ACE=∠BCF,
∴∠ACE+∠ACF=∠BCF+∠ACF=90°,
∴∠ECF=90°,
∴△ECF是等腰直角三角形,
∴OC=OE且OC⊥OE;
(2)(1)的结论成立,
如图②,延长EO到F使OF=OE,连接EC,BF,CF,
在△DOE与△BOF中,$\left\{\begin{array}{l}{DO=BO}\\{∠DOE=∠BOF}\\{EO=FO}\end{array}\right.$,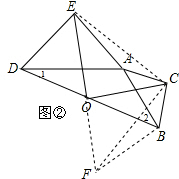
∴△DOE≌△BOF,
∴DE=BF,∠EDO=∠OBF=∠EDA+∠1,
∴AE=BF,
∵△ABC与△ADE都是等腰直角三角形,∠ACB=∠AED=90°,
∴∠EDA=∠ABC=∠EAD=∠CAB=45°,
∴∠CBF=45°+∠2+45°+∠1=90°+∠1+∠2,
∠CAE=360°-∠DAB-90°=270°-(180°-∠1-∠2)=90°+∠1+∠2,
∴∠CAE=∠CBF,
在△ACE与△BCF中,$\left\{\begin{array}{l}{AE=BF}\\{∠EAC=∠FBC}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCF,
∴EC=CF,∠ACE=∠BCF,
∴∠ACE+∠ACF=∠BCF+∠ACF=90°,
∴∠ECF=90°,
∴△ECF是等腰直角三角形,
∴OC=OE且OC⊥OE.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 65° | B. | 60° | C. | 45° | D. | 70° |
 有一个直径为a+b的圆形公园,挖去直径分别为a与b的两个圆形荷花池,剩下的地方全部植草皮,问草皮的面积是多少?
有一个直径为a+b的圆形公园,挖去直径分别为a与b的两个圆形荷花池,剩下的地方全部植草皮,问草皮的面积是多少?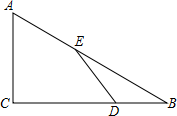 如图,Rt△ABC中,∠C=90°,∠B=30°,BA=6,点E在AB边上,点D是BC边上一点(不与点B、C重合),且AE=ED,线段AE的最小值是( )
如图,Rt△ABC中,∠C=90°,∠B=30°,BA=6,点E在AB边上,点D是BC边上一点(不与点B、C重合),且AE=ED,线段AE的最小值是( )