题目内容
18.不等边三角形的两条边上的高分别为4和12,若第三条边上的高的长也是整数,则这个整数的最大值是5.分析 设角形三边分别为a,b,c,面积为S,根据三角形面积公式分别用含S的代数式表示出a、b、c,根据三角形三边之间的关系得a-b<c<a+b,列出不等式后解不等式可得.
解答 解:设三角形三边分别为a,b,c,面积为S,
则a=$\frac{2S}{4}$,b=$\frac{2S}{12}$,c=$\frac{2S}{h}$,
∵a-b<c<a+b,
∴$\frac{2S}{4}-\frac{2S}{12}<\frac{2S}{h}<\frac{2S}{4}+\frac{2S}{12}$,
解得:3<h<6,
故h=4或5,
又∵三角形是不等边三角形,
∴h=5.
故答案为:5.
点评 本题主要考查三角形面积及三边之间的关系,利用三角形的面积公式表示出三边长度是前提,根据三边间的关系列出不等式组是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
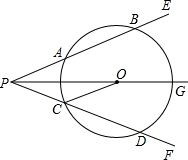 如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE
如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE
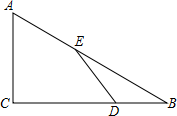 如图,Rt△ABC中,∠C=90°,∠B=30°,BA=6,点E在AB边上,点D是BC边上一点(不与点B、C重合),且AE=ED,线段AE的最小值是( )
如图,Rt△ABC中,∠C=90°,∠B=30°,BA=6,点E在AB边上,点D是BC边上一点(不与点B、C重合),且AE=ED,线段AE的最小值是( )