题目内容
5．已知$\sqrt{x}$+$\frac{1}{\sqrt{x}}$=2，那么$\sqrt{\frac{x}{{x}^{2}+2x+1}}$-$\sqrt{\frac{x}{{x}^{2}+7x+1}}$=$\frac{1}{6}$．分析 先求出：x+$\frac{1}{x}$=2，再用整体代入的方法解决问题．
解答 解：∵$\sqrt{x}$+$\frac{1}{\sqrt{x}}$=2，
∴x+$\frac{1}{x}$+2=4，
∴x+$\frac{1}{x}$=2，
∴原式=$\sqrt{\frac{1}{x+2+\frac{1}{x}}}-\sqrt{\frac{1}{x+7+\frac{1}{x}}}$=$\frac{1}{2}-\frac{1}{3}$=$\frac{1}{6}$，
故答案为$\frac{1}{6}$．
点评 本题考查二次根式的化简，关键是灵活运用公式，学会整体代入的解题思想，有一定的技巧．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16．
如图所示，与∠B构成同位角的共有（ ）
如图所示，与∠B构成同位角的共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
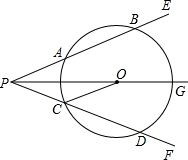如图所示，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OC∥PE
有一个直径为a+b的圆形公园，挖去直径分别为a与b的两个圆形荷花池，剩下的地方全部植草皮，问草皮的面积是多少？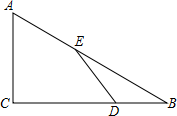
如图，Rt△ABC中，∠C=90°，∠B=30°，BA=6，点E在AB边上，点D是BC边上一点（不与点B、C重合），且AE=ED，线段AE的最小值是（ ）